1. Talsystemer
Når man skal studere et abstrakt begreb, som talsystemer, er det en god idé at starte med, hvad man kender til emnet fra det praktiske liv.
Igennem tiderne har man brugt forskellige talsystemer. Det mest kendt af de forgangne er nok romertallene. Romertallene er opbygget på en speciel måde. I romertal bruges symboler som: I, V, X, C, M osv. F.eks. er IV et romertal.
I = 1
V = 5
X = 10
C = 100
M = 1.000
Man skal følge nogle specielle regneregler:
| Man evaluerer først alle symboler, der er ens, og som står umiddelbart ved siden af hinanden. |
| Hvis A<B skal A trækkes fra, i det samlede regnestykke. F.eks. bliver IV til -1+V = -1+5 = 4 |
| Hvis A>B skal B lægges til, i det samlede regnestykke. F.eks. bliver VIII til V+3 = 5+3 = 8 |
|
Symboler
|
Alle talsystemer har en række symboler med individuel værdi, som på en eller anden måde indgår i fortolkningen af et tals repræsentation i det pågældende talsystem. |
|
Værdi
|
Værdien af et tal er abstrakt. Vi kan kun udtrykke værdien af et tal, i et hvilket som helst talsystem, ved at repræsentere det i et andet talsystem. Der findes dermed ikke nogen "rigtig" måde at angive en værdi på. |
|
Rækkefølge eller position
|
Symbolerne er angivet i en bestemt rækkefølge, og skal fortolkes ud fra denne rækkefølge. Det være sig, som det er tilfældet for romertal, deres relative position eller som vi skal se nedenfor deres absolutte position. |
Vi bruger normalt 10-talssystemet, også kaldet det decimale system. 10-talssystemet kalder også araber-tal, da de stammer fra de arabiske matematikere. Tallet 10 er grundtallet i vores talsystem; hvilket med al overvejende sandsynlighed kommer af, at vi har ti fingre. Men hvad betyder det, at grundtallet er 10?
Hvis man ser nærmere på et vilkårligt tal, f.eks. 4175, kan det udtrykkes som 4 tusinder, 1 hundrede, 7 tiere og 5 enere. At dette er et tal i 10-talssystemet ses af, at det der tælles: tusinder, hundrede, tiere og enere kan skrives som potenser af 10. Lad os se det skematisk:
Decimalt eksempel
|
Decimalt ciffer |
4 |
1 |
7 |
5 |
|
Positions navn |
tusinde |
hundrede |
tiere |
enere |
|
Positions værdi |
1.000 |
100 |
10 |
1 |
|
Positions værdi som potens af 10 |
103 |
102 |
101 |
100 |
Tallet 10 kaldes grundtallet, og er afgørende for, hvordan en række cifre skal fortolkes som værdi.
Bit
I en computer arbejder vi med symboler bestående af kombinationer af strøm og mangel på strøm. Vi plejer at notere disse kombinationer som et-taller (strøm) og nuller (ingen strøm), og vi kalder hver af disse for en bit. Hvordan skal man så repræsentere tal med disse kombinationsmuligheder?
Hvis vi i første omgang skal prøve at holde os til 10-talssystemet er spørgsmålet, hvor mange bit, der skal til for at lave ti forskellige kombinationer. Med en bit kan vi lave 2 kombinationer: 0 og 1. Med to bit kan vi lave 4 kombinationer: 00, 01, 10 og 11. Hver gang vi føjer en bit mere til kan vi lave dobbelt så mange kombinationer. Det er fordi vi med den næste bit kan lave to, og for hver af dem de samme som før vi føjede den til. Man kan derfor beregne antallet af kombinationsmuligheder som 2 opløftet til antallet af bit. Med 3 bit, 23 = 8 kombinationer. Endnu ikke nok til at repræsentere et ciffer i titalssystemet, men med 4 bit, 24 = 16 kombinationer får vi nok og lidt ekstra. Vi kan derfor bruge 4 bit til at repræsentere ét ciffer i 10-talssystemet. Hvis vi skal repræsentere et to-cifret tal skal vi bruge 8 bit osv.
At repræsentere decimale tal på denne måde, med 4 bit, er umiddelbart i orden, men der går 6 kombinationer til spilde. Med ét ciffer giver det et spild på 6/16 = 37,5%, med to cifre (256-100)/256 = 60,9%, med tre cifre (4096-1000)/4096 = 75,6%, osv. Vi kan konstatere, at store tal repræsenteret på denne måde giver et enormt spild af kombinationer. Denne repræsentationsform kaldes binary coded decimal (BCD) og bliver anvendt, men kun i meget begrænset udstrækning. Hvad kan man ellers gøre?
Hvis man skriver en kombination af f.eks. 4 bit, det kunne være 0101, ser man, at der er fire pladser, hvor der kan stå enten 0 eller 1. Et decimalt tal er bygget op på samme måde, men her kan der på hver plads stå et af ti forskellige tegn. Vi valgte at fortolke 4175 som et decimalt tal, men vi kan også vælge at fortolke 0101 som et decimalt tal, nemlig 101. Da det kan være lidt vanskeligt at se om vi mener en kombination af 3 bit eller tallet 101, vil vi fremover skrive decimale tal som 101D, hvor det lille D står for Decimalt. Vi kunne også vælge at fortolke 0101 anderledes!
I 10-talsystemet findes der 10 mulige cifre/tegn. En bit kan være enten 0 eller 1, altså to mulige tegn, som vi kan fortolke som cifre. Med 2 mulige cifre vil det være naturligt at fortolke det som et tal i 2-talsystemet! 2-talsystemet kaldes også det binære talsystem. Lad os se det samme skema for 2-talsystemet, som vi lavede for 10-talsystemet.
Binært eksempel
|
Binært ciffer |
0 |
1 |
0 |
1 |
|
Positions navn |
ottere |
firere |
toere |
enere |
|
Positions værdi |
8 |
4 |
2 |
1 |
|
Positions værdi som potens af 2 |
23 |
22 |
21 |
20 |
Man kan derfor beregne 0101's decimale værdi som: 0*8+1*4+0*2+1*1 = 5D .
Det binære talsystem er det, der er det mest naturlige for computere som vi kender dem i dag. Ordet "bit" betyder BInary digiT, binært ciffer. Vi vil i det følgende, analogt til decimal tal, skrive binære tal som, f.eks. 0101B for at kende dem fra de decimale.
1.1 Omskrivning til octalt/hexadecimalt
Der er dog et mindre problem med de binære tal: De fylder! f.eks. er 4175D binært 1.0000.0100.1111B, hvilket er upraktisk langt. F.eks. er det ikke egnet til at blive udtalt!
Man kunne omregne det til det decimale tal 4175D og bruge det, og så lave omregningen frem og tilbage efter behov. Det viser sig dog at være en meget dårlig idé. Det skyldes at 2-talssystemet og 10-talsystemet er meget skæve i forhold til hinanden. Det er simpelthen besværligt!
Der er ikke noget lettere for mennesker at forstå end decimal-tal. Når vi i stedet vælger en anden repræsentation, end den decimale, til at håndtere binære tal må vi derfor ikke forvente, at den bliver lige så let at forstå. Vi forlanger kun, at det er let at omregne mellem binært og denne repræsentation, samt at den er nemmere at håndtere end de lange bit-strenge.
Vi vælger derfor et nyt talsystem, med et andet grundtal end 10, til at løse denne opgave for os, men hvilket? For at give os så meget som muligt en fornemmelse af, hvad tallet er decimalt og specielt, at vi kan bruge de kendte cifre 0, ... , 9 må vi vælge et grundtal på ca. 10. Vi så tidligere, at et decimalt ciffer passede dårligt med det antal bits (vi fik, at vi skulle bruge 4 bit = 16 kombinationer, altså et dårligt match!), der skulle til for at repræsentere det. Vi vil derfor vælge et talsystem der passer præcist med antallet af kombinationer for et vist antal bits. 4 bit gav 16 kombinationer, så 16-talsystemet er en mulighed. 3 bit giver 8 kombinationer, så 8-talsystemet er også en mulighed.
16-talsystemet kaldes det hexadecimale talsystem, eller blot hex! Det har den ulempe, at man i modsætning til 8-talsystemet, ikke kan nøjes med cifrene 0, ..., 9. Man vælger at bruge bogstaverne A, ..., F for cifrene 10D, ..., 15D .
Vi kan nu lave en samlet opstilling med alle cifrene for vores fire talsystemer:
Cifre i talsystemerne
|
Binært |
Octalt |
Decimalt |
Hex |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
3 |
3 |
3 |
|
|
4 |
4 |
4 |
|
|
5 |
5 |
5 |
|
|
6 |
6 |
6 |
|
|
7 |
7 |
7 |
|
|
8 |
8 |
||
|
9 |
9 |
||
|
A |
|||
|
B |
|||
|
C |
|||
|
D |
|||
|
E |
|||
|
F |
Som det ses kaldes 8-talssystemet også for det octale talsystem. Man kan ligeledes lave tabeller som vi gjorde for det decimale og det binære talsystem .
I det octale talsystem bliver vores eksempel 4175O.
Octalt eksempel
|
Octalt ciffer |
4 |
1 |
7 |
5 |
|
Positions værdi |
512 |
64 |
8 |
1 |
|
Positions værdi som potens af 8 |
83 |
82 |
81 |
80 |
Vi kan her beregne, at 4175O = 4*512+1*64+7*8+5*1 = 2173D . Ved umiddelbart at sammenligne de to tal ses, at det octale er "større" end det decimale. Det vil altid være således, da vi har færre mulige cifre i det octale, og derfor må bruge flere cifre for at få det samme antal kombinationer!
I det hexadecimale talsystem bliver vores eksempel 4175H.
Hexadecimalt eksempel
|
Hexadecimalt ciffer |
4 |
1 |
7 |
5 |
|
Positions værdi |
4096 |
256 |
16 |
1 |
|
Positions værdi som potens af 16 |
163 |
162 |
161 |
160 |
Vi kan her beregne, at 4175H = 4*4096+1*256+7*16+5*1 = 16.757D . Her får vi i modsætning til det octale talsystem, at hex er kortere end decimalt. Det skyldes at hex har seks mulige cifre mere end det decimale, og vi derfor kan skrive flere kombinationer med det samme antal cifre.
Den observerede sammenhæng mellem antal cifre og mulige cifre, kan man også se når man studerer "den lille tabel":
"Den lille tabel"
|
Binært |
Octalt |
Decimalt |
Hex |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
10 |
2 |
2 |
2 |
|
11 |
3 |
3 |
3 |
|
100 |
4 |
4 |
4 |
|
101 |
5 |
5 |
5 |
|
110 |
6 |
6 |
6 |
|
111 |
7 |
7 |
7 |
|
1000 |
10 |
8 |
8 |
|
1001 |
11 |
9 |
9 |
|
1010 |
12 |
10 |
A |
|
1011 |
13 |
11 |
B |
|
1100 |
14 |
12 |
C |
|
1101 |
15 |
13 |
D |
|
1110 |
16 |
14 |
E |
|
1111 |
17 |
15 |
F |
|
10000 |
20 |
16 |
10 |
Det er en god idé at studere denne tabel grundigt.
Det første man observerer er, hvor dårligt det decimale passer sammen med de andre. Det skyldes netop, at vi har valgt det octale og det hexadecimale for, at det skulle passe med det binære, hvorved de "arver" det dårlige forhold mellem det binær og det decimale talsystem. Det er f.eks. tydeligt i den nederste linie, hvor de tre andre er pæne tal: 10000B , 20O og 10H , og det decimale er 16D!
Nu var argumentet for at indføre det octale og det hexadecimale talsystem at det var nemt at omregne til og fra det binære. Det er utrolig enkelt! Hvis man vil omregne fra binært til octalt, skriver man det binære tal op, og sætter en prik mellem hver tredie, startende fra højre. F.eks.:
|
1.000.001.001.111 |
For hver gruppe af 3 bit skriver man det tilsvarende octale ciffer fra "den lille tabel":
|
1. 0. 1. 1. 7 |
Altså er 1000001001111B = 10117O . Man kommer den anden vej fuldstændig analogt. For omregning med det hexadecimale talsystem deler man blot i blokke af fire; hvilket med det samme binære tal giver:
|
1.0000.0100.1111 1. 0. 4. F |
Og dermed, at 1000001001111B = 104FH .
Det octale talsystem er det mindst brugte af de fire. Man skulle umiddelbart tro, at det hexadecimale var det mindst brugte pga. af ulempen med de ekstra mulige cifre. Sådan var det også i begyndelsen men én bestemt ting gjorde, at hex for tiden er det mest udbredte: Byten! I de fleste computere er data opdelt i bytes (8 bit) eller multiplum af otte, f.eks. 16 og 32. Da det octale talsystem samler 3 bits af gangen og hex 4 bit, er det afgørende, at 4 går op i 8, mens 3 ikke gør! Et eksempel på, at det octale kan være praktisk er fileadgangsbeskyttelsen i UNIX med de tre "cifre" r, w og x.
Vi har nu set hvorledes man let kan omskrive mellem binært« octalt og binært« hex. Vi har dermed fået en mere praktisk måde at notere binære tal på, men vi har stadig problemet med at omregne mellem det binære og det decimale!
1.2 Omregning til/fra decimalt
1.2.1 Den positionelle metode
Vi har allerede anvendt en teknik for octal og hex (for at studere dem) som også kan bruges på omregning fra binær til decimal. Metoden er den positionelle metode. Hver position i tallet har en bestemt positionsværdi, som ganges med det ciffer der står på positionen og man summerer det hele. Lad os se en række af de binære positionsværdier:
Binære positions-værdier
|
Pos. |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Pos.-værdi |
32768 |
16384 |
8192 |
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
Pos.værdi 2-potens |
215 |
214 |
213 |
212 |
211 |
210 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
Hvis vi f.eks. ville omregne 1.0000.0100.1111B til decimalt kunne det gøres ved at summere alle positionsværdierne for 1'erne i det binære tal, altså: 4096+64+8+4+2+1 = 4175D . Man kan ikke bruge den positionelle metode den anden vej, for hvad er den binære positionsværdi for 7 i 4175? Man kan i stedet bruge den tilnærmede positionelle metode.
Den tilnærmede positionelle metode forløber som følger: Hvilken positonsværdi kommer tættest på 4175D uden at overstige den? Det gør 4096, der svarer til position 12. Vi sætter et 1-tal på position 12, trække 4096 fra 4175 og arbejde videre med resultatet. Den samlede udregning ser ud som følger:
|
4175 |
(12)+(6)+(3)+(2)+(1)+(0) = 1.0000.0100.1111 |
Ovenfor er i parentes angivet på hvilket positioner der skal sættes en bit. Når vi f.eks. trækker 64 fra 79 skal vi derfor sætte en bit på position 6 da 64 = 26.
1.2.2 Forskydningsmetoden
I stedet for de positionelle metoder kan man også bruge forskydningsmetoden. Forskydningsmetoden egner sig bedst til programmer. Det skyldes at den er meget enkel at udføre i sine skridt, men der er til gengæld mange af dem. Den kan dog også (med påpasselighed og hovedet under armen) bruges manuelt.
På grund af metodens mange skridt vil vi indskrænke os til at omforme det binære tal 1101B .
Lad os igen starte med at omregne fra binært til decimalt, og lad os først se hele processen:
|
(3) 1 |
Man kunne også skrive denne udregning som: (((((1)*2)+1)*2)+0)*2)+1 = 13. Idéen er, at man "skubber" det binære tals cifre ind i det decimale med "hastigheden" 2.
Skal man den anden vej: fra decimal til binær skubber man den anden vej, dvs. man dividerer med 2:
|
13/2 = 6 og rest 1 |
Man læser nu resterne, nede fra og op og resultatet er 1101B .
Hvilket talsystem skal man så bruge: binært, octalt eller hex? Det kommer helt an på situationen. Man skal ikke føle sig bundet til en bestemt.
Mht. omregningsmetoder skal man også vælge den der forekommer mest praktisk i den pågældende situation. Hvis man laver et program til omregning, vil man dog finde at forskydningsmetoden er den mest enkle.
2. Negative tal
Vi er nu i stand til at repræsentere tallene fra 0 op til hvad som helst, bare vi bruger bits nok. Men hvad med negative tal? Vi skal se på flere forskellige metoder, ikke alle lige hensigtsmæssige!
Den første idé man kunne få, ville være at bruge en bit til at angive om tallet skulle regnes for negativt eller positivt. Det ville altså kræve en ekstra bit ud over dem der angiver "tallet". Da et fortegn altid står forrest, ville det være naturligt at sætte denne bit foran "tallet". Lad os indskrænke os til at arbejde med 3 bit, hvoraf den ene er fortegnsangivelsen. Med denne konstruktion ville vi kunne repræsentere flg. værdier:
Fortegns-bit
|
Decimalt |
Fortegns-bit |
|
0 |
000 |
|
1 |
001 |
|
2 |
010 |
|
3 |
011 |
|
-0 |
100 |
|
-1 |
101 |
|
-2 |
110 |
|
-3 |
111 |
Ovenfor er tallene opstillet i rækkefølge efter de 3 bits fortolket som et positivt tal. Det viser os nemlig en række fænomener der kan give grund til bekymring: Der er to nuller! Både et plus nul og et minus nul. Men det værste: Efter -0 kommer -1 og ikke 1! Det synes måske umiddelbart at være ugennemskueligt, hvorfor det skulle været et problem, men man skal tænke på hvor anvendelig repræsentationen er. Da det er tal vi arbejder med at repræsentere, skal vi på et tidspunkt kunne regne med dem. Lad os se hvordan man adderer, f.eks. 01100111B med 00111001B:
|
1111111 |
Eksemplet er med vilje valgt så der kommer mange menter for at understrege, at der regnes fuldstændig normalt med binære tal som med alle andre tal. Når vi vil lave en repræsentation af negative tal vil det være hensigtsmæssigt hvis et meget positivt tal f.eks. 35 og et ikke så negativt tal, f.eks. -4, lagt sammen gav en bit-repræsentation, der svarede til 31. Lad os se et regne-eksempel taget fra vores 3 bit repræsentation. Vi vil lægge 2 og -1 sammen:
|
010 2 |
Her blev der ingen menter, men bemærk, hvad 111 er i vores 3 bit repræsentation: -3! Det dur ikke, vi kan ikke blot regne med repræsentationen som om den forreste bit var et almindeligt binært ciffer. Nu er den forreste bit ikke et binært ciffer, så det synes måske ikke så skuffende: "Hvorfor skulle vi kunne gøre det, når det netop ikke er et binært ciffer?". Svaret er, at det ville være praktisk ikke at skulle behandle de negative tal specielt ved regning. Men er det muligt? Under alle omstændigheder må vi så kassere denne fortegns-bit repræsentation.
For at få en idé om hvad der grundlæggende er galt med vores repræsentation vil vi kort se på temperaturskalaer.
De fleste er nok bekendt med Celsius-skalaen med 0°C for vands frysepunkt og 100°C for vands kogepunkt. Ligeledes har de fleste nok hørt om Farenheit-skalaen, men de færreste kan regne med den. Det er også ligegyldigt i denne sammenhæng for den skala vi vil stille op over for Celsius-skalaen er ikke Farenheit men Kelvin1. Kelvin-skalen har nemlig den fordel, at den har samme ækvidistance som Celsius-skalen. Dvs. at stiger temperaturen en grad Celsius, stiger den også en grad Kelvin. Forskellen er, at Kelvin-skalaen starter ved det absolutte nulpunkt -273°C. Da der ikke findes temperaturer under det absolutte nulpunkt betyder det at Kelvin-skalaen kun har positive værdier.
Situationen er lidt den sammen som med vores binære tal. Vi har vores "Kelvin-skala": vores positive tal. Men vil nu have en "Celsius-skala", med både positive og negative tal. Lad os stille Celsius-skalaen op over for Kelvin-skalen så vi bedre kan gennemskue problemstillingen:
Kelvin og Celcius temperaturer
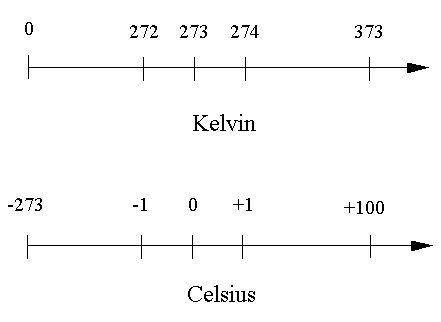 |
Skalaerne er lidt fortegnede for at kunne se nogle interessante temperaturer omkring Celsius' nulpunktet. Først ser man, at der kun er ét nul på Celsius-skalaen, og man ser, at regnet på Kelvin skalen kommer -1°C, 0°C og +1°C efter hinanden. Det gjorde de ikke i vores repræsentation med fortegns-bit! Når man lægger tal sammen er dette afgørende, hvis man skal får det rigtige resultatet i repræsentationen. Vi skal derfor ændre vores repræsentation så dette kommer til at passe. Hvis vi ser på vores skema fra før, skal bit-kombinationerne komme i samme rækkefølge, men vi skal ændre vores fortolkning af dem:
Excess
|
Decimalt |
Excess |
|
-4 |
000 |
|
-3 |
001 |
|
-2 |
010 |
|
-1 |
011 |
|
+0 |
100 |
|
+1 |
101 |
|
+2 |
110 |
|
+3 |
111 |
Ligesom Celsius-skalaen kan forskydes i forhold til Kelvin-skalaen og stadig indeholde både positive og negative tal, således kan vi også vælge at forskyde vores fortolkning af repræsentationen. Ovenstående fortolkning kaldes excess. Lad os undersøge repræsentationen.
For det første er der kun et nul! Men kan man regne med det. Lad os f.eks. prøve (0 + -1)
|
100 0 |
Hvilket er +3. Det dur stadig ikke! Problemet er at de negative tal bringer os frem, og ikke tilbage på skalaen.
Det er ikke overraskende da 0°C plus -1°C på Kelvin skalen giver 545! For at komme videre må vi gå en anden vej.
Hvad sker der hvis man lægger 1 til den største værdi vi kan have med 3 bit som binære cifre?
|
111 |
Vi får en værdi der falder uden for vores repræsentation. Hvis vi blot smider den ekstra foreste bit væk står der 000, altså er vi kommet tilbage til starten igen! Hvis man regner på denne måde kommer vores repræsentation til at virke som en tallinie der er bøjet rundt i en cirkel:
Figur 2:
Tallinie bøjet omkring cirkel
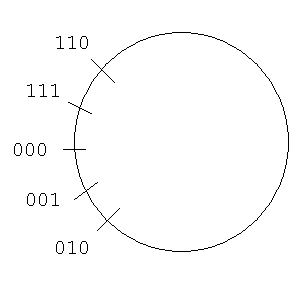 |
Men hvordan skal vi udnytte dette? Man bemærker at 111B+001B = 000B . Altså har 111B den samme virkning som vi ønsker -1 skal have. Hvad skal så være -2? Man skal løse den binære ligning X+010B = 000B . Den har løsningen 110B . Dette ses ved at løse ligningen en bit af gangen fra højre mod venstre! 110B er én mindre end 111B , Hvorfor -3 analogt er 101B osv. Det giver følgende repræsentation:
2. komplement
|
Decimalt |
2. Komplement |
|
0 |
000 |
|
+1 |
001 |
|
+2 |
010 |
|
+3 |
011 |
|
-4 |
100 |
|
-3 |
101 |
|
-2 |
110 |
|
-1 |
111 |
I forhold til vores første forsøg med fortegns-bit er de negative tals rækkefølge vendt, og -0 er nu udnyttet til et ekstra negativt tal. Man bemærker også, at man ud fra den binære repræsentation stadig kan se om tallet er positivt eller negativt ved, at se på den forreste bit. Ovenstående repræsentation virker, men hvordan kommer man fra den ene til den anden? Det gøres ved at negere tallet og lægge én til. Se f.eks. i tabellen mht. +2 og -2: 010B negeret er 101B og med én lagt til bliver det 110B; hvilket er -2 i tabellen. Når man vil den anden vej gøres nøjagtig det samme.
Repræsentationen kaldes 2. komplement. Der findes også en form der hedder 1. komplement, den ser ud som:
1. komplement
|
Decimalt |
1. Komplement |
|
0 |
000 |
|
+1 |
001 |
|
+2 |
010 |
|
+3 |
011 |
|
-3 |
100 |
|
-2 |
101 |
|
-1 |
110 |
|
-0 |
111 |
Man bemærker at der her er to nuller. Til gengæld er værdimængden symetrisk omkring nul; hvilket den ikke er for 2. komplement, hvor der er et negativt tal mere end der er positive. 1. komplement fås ved blot at negere. Når man beregner 2. komplement laver man derfor først 1. komplement og lægger derefter én til!
Hvor utroligt det end lyder kan man regne næsten almindeligt med 1. komplement tal. I modsætning til 2. komplement, hvor man smider en overskudende mente væk, lægger man den i 1. komplement til resultatet! Lad os se et eksempel:
|
11 |
Hvor -1+2 = +1.
Vi har nu set fire muligheder for at repræsentere negative tal: Fortegns-bit, excess, 1. og 2. komplement. Den der bruges er 2. komplement, da den kun har ét nul og man kan regne "normalt" med den!
3. Radix specifikation
Når man angiver tal i assembler har man behov for entydigt at specificere, hvilket talsystem angivelsen skal fortolkes i. Det gøres ved at sætte et bogstav efter tallet.
Decimal-tal er default, men man kan alligevel vælge at sætte et 'D' efter for at tydeliggøre for læseren af programmet, at der er tale om et decimal-tal, f.eks.:
|
MOV AX, 100D |
Binært angives med bogstavet 'B' og hex med 'H'. I forbindelse med hex skal man være opmærksom på et entydighedsproblem. F.eks.:
|
MOV BL, AH |
Registrene AH, BH, CH og DH kan også fortolkes som AH, BH, CH og DH. Assembleren vil vælge at fortolke dem som registre. Man løser problemet ved at foranstille et 0; hvorved hex-værdien er den samme, men det ikke længere kan forveksles med et register. Man bør derfor gøre det til en god vane altid at sætte et 0 foran alle hex-værdier, da det kan være en vanskelig fejl at finde.
Det er ikke muligt at angive octale tal i Intel-assembler.
Det er uden betydning om bogstaverne er store eller små. F.eks. kan man bruge flg.:
|
MOV AX, 4Eh |
4. Binary coded decimal
[Mangler]
Fodnoter
Repetitionsspørgsmål
Opgaver
Skriv følgende binære tal på henholdsvis octal og hexadecimal form.
|
a:
|
01001100 |
|
b:
|
01101111 |
|
c:
|
01001110 |
|
d:
|
00110100 |
|
e:
|
01000100 |
|
f:
|
01101011 |
|
g:
|
01001010 |
Omregn de binære tal, fra opgave 1, til decimalt med:
|
a:
|
Den positionelle metode. |
|
b:
|
Forskydningsmetoden. |
Beregn den binære repræsentation af flg. tal ved 2. komplement (med 8 bit).
|
a:
|
-1
|
|
b:
|
-128
|
|
c:
|
-4
|
|
d:
|
-64
|
|
e:
|
101
|
Beregn den decimale repræsentation af flg. binære tal, der er angivet i 2. komplement:
|
a:
|
11100100 |
|
b:
|
00111110 |
|
c:
|
10000001 |
|
d:
|
10001111 |
Udregn følgende regnestykker i de talsystemer de er angivet i. Dvs. uden at gå over i andre talsystemer som mellemregning.
|
a:
|
1101B + 10001011B |
|
b:
|
771O + 1132O |
|
c:
|
AF12H + EAAFH |
|
d:
|
11110B + 11B |
|
e:
|
317O + 71O |
|
f:
|
9011H + FFH |
Svar på repetitionsspørgsmål
Vejledende løsninger til opgaverne
|
Opg.
|
Octal inddeling
|
Octalt
|
Hex inddeling
|
Hex
|
|
a
|
01.001.100
|
114O
|
0100.1100
|
4CH
|
|
b
|
01.101.111
|
157O
|
0110.1111
|
6FH
|
|
c
|
01.001.110
|
116O
|
0100.1110
|
4EH
|
|
d
|
00.110.100
|
064O
|
0011.0100
|
34H
|
|
e
|
01.000.100
|
104O
|
0100.0100
|
44H
|
|
f
|
01.101.011
|
153O
|
0110.1011
|
6BH
|
|
g
|
01.001.010
|
112O
|
0100.1010
|
4AH
|
|
Opg.
|
Den positionelle metode
|
|
a
| 64 + 8 + 4 = 76 |
|
b
| 64 + 32 + 8 + 4 + 2 + 1 = 111 |
|
c
| 64 + 8 + 4 + 2 = 78 |
|
d
| 32 + 16 + 4 = 52 |
|
e
| 64 + 4 = 68 |
|
f
| 64 + 32 + 8 + 2 + 1 = 107 |
|
g
| 64 + 8 + 2 = 74 |
I det følgende, er det andet foranstillede 0 i opgave d bevaret, for at fremhæve ensartetheden i forløbet.
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
|
1 |
1 x2 ---- 2 +1 ---- 3 x2 ---- 6 +0 ---- 6 x2 ---- 12 +1 ---- 13 x2 ---- 26 +1 ---- 27 x2 ---- 54 +1 ---- 55 x2 ---- 110 +1 ---- 111 |
1 x2 ---- 2 +0 ---- 2 x2 ---- 4 +0 ---- 4 x2 ---- 8 +1 ---- 9 x2 ---- 18 +1 ---- 19 x2 ---- 38 +1 ---- 39 x2 ---- 78 +0 ---- 78 |
0 x2 ---- 0 +1 ---- 1 x2 ---- 2 +1 ---- 3 x2 ---- 6 +0 ---- 6 x2 ---- 12 +1 ---- 13 x2 ---- 26 +0 ---- 26 x2 ---- 52 +0 ---- 52 |
1 x2 ---- 2 +0 ---- 2 x2 ---- 4 +0 ---- 4 x2 ---- 8 +0 ---- 8 x2 ---- 16 +1 ---- 17 x2 ---- 34 +0 ---- 34 x2 ---- 68 +0 ---- 68 |
1 x2 ---- 2 +1 ---- 3 x2 ---- 6 +0 ---- 6 x2 ---- 12 +1 ---- 13 x2 ---- 26 +0 ---- 26 x2 ---- 52 +1 ---- 53 x2 ---- 106 +1 ---- 107 |
1 x2 ---- 2 +0 ---- 2 x2 ---- 4 +0 ---- 4 x2 ---- 8 +1 ---- 9 x2 ---- 18 +0 ---- 18 x2 ---- 36 +1 ---- 37 x2 ---- 74 +0 ---- 74 |
Opgave a-d er simple at omregne til binært, da 1, 128, 4 og 64 er 2-potenser. Opgave e er en almindelig omregning, med den tilnærmede positionelle metode.
|
a: 00000001 b: 10000000 |
c: 00000100 d: 01000000 |
e: 101 altså: 65 2 0 |
|
a: 11100100 16 + 8 + 4 = -28D b: 00111110 32 + 16 + 8 + 4 + 2 = 62D |
c: 10000001 128 - 1 = -127D d: 10001111 64 + 32 + 16 + 1 = -113D |
|
a: 1111 b: 11 |
c: 1 1 d: 111 |
e: 11 c: 11 |