1. Node-klassen

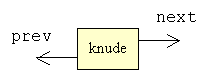
Knude

I en dobbelthægtet liste, har hver knude (eng.: node) ikke alene en reference til den næste, men også en til den foregående knude.

Vi vil implementere en sådan knude på følgende måde

Node.java

public class Node {
  private Object data;
  protected Node prev, next;
  
  public Node( Object data ) {
    this( data, null, null );
  }
  
  public Node( Object data, Node prev, Node next ) {
    this.data = data;
    this.prev = prev;
    this.next = next;
  }
  
  public Object getData() {
    return data;
  }
}

Package

For at gøre knuden mere generel, har vi valgt at lade dens tilhørende data kunne være et hvilket som helst objekt, idet vi har bruget en Object-reference. Vi har valgt at lade next og prev være protected, så andre klasser i samme package kan tilgå dem direkte. Dette er bekvemt i forbindelse med den container-klasse, vi senere skal konstruere, samtidig med at protected beskytter datakernen mod klienten. Vi vil ikke her nærmere specificere hvad denne package skal hedde, men det er i det følgende underforstået, at alle klasserne tilhører en sådan package, pånær testanvendelser (Main.java), der altid vil være placeret udenfor.

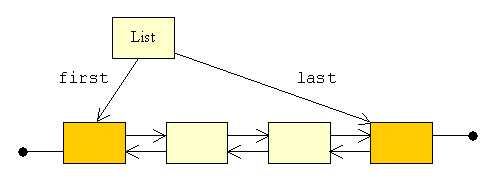
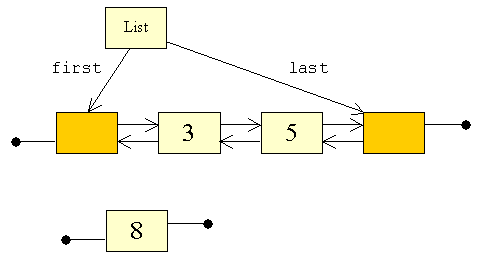
Når vi opbygger en liste af knuder, placerer vi en dummy i hver ende:

Disse dummies bidrager til at gør indsættelse/sletning af knuder ensartet, uanset hvor i listen vi ønsker at indsætte/slette. Denne ensartethed gør implementationen af de pågældende operationer enklere.

Man bemærker, at vi lader såvel prev i den første dummy, som next i den sidste dummy, være null. Dette bruges som en indikation af, at listen ikke er længere i den pågældende retning.

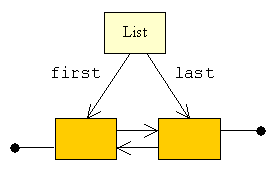
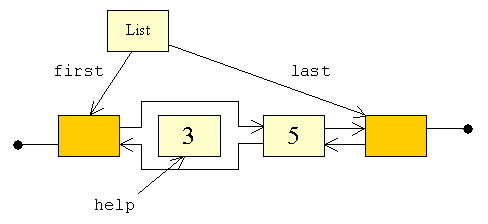
Som man ser, er listen symmetrisk. Denne symmetri bevirker, at det er nærliggende at arbejde med begge ender af listen. For at lette en sådan tilgang til, ikke alene starten, men også slutningen af listen, holder vi fast i den med to referencer:

Med first og last kan vi nu hurtigt tilgå begge ender af listen.

2. List-klassen

Der forestår nu den opgave at designe og implementere List-klassen, der som container-klasse vil repræsentere datastrukturen overfor klienter. Det vil samtidig være denne klasse, der foretager operationer på listen.

Datakerne og konstruktor får følgende udformning:

List.java

public class List {
  private Node first, last;
  private int size;
  
  public List() {
    first = new Node( null );
    last = new Node( null );
    
    first.next = last;
    last.prev = first;
    
    size = 0;
  }
  
  public int size() {
    return size;
  }
  
  public boolean empty() {
    return size == 0;
  }
  
  // access-metoder
}

Ud over first- og last-referencerne, vil vi også registrere, hvor mange elementer der er i listen. Dette gøres med en simpel tæller: size, der holdes ajour af access-metoderne. En sådan tæller gør det nemt at implementere size- og empty-metoderne.

I konstruktoren opbygger vi en tom liste:

Idet data-referencen i de to dummies sættes til null, da de ikke skal anvendes.

2.1 toString

Da vi løbende har behov for at teste diverse access-metoder, har vi allerede fra starten behov for en toString-metode, der kan vise os listens indhold. En sådan metode kan implementeres på følgende måde:

List.java

public String toString() {
  StringBuffer sb = new StringBuffer();
  
  sb.append( "[List:" );
  
  for ( Node n = first.next; n!=last; n = n.next )
    sb.append( " " + n.getData() );
  
  sb.append( "]" );
  
  return sb.toString();
}

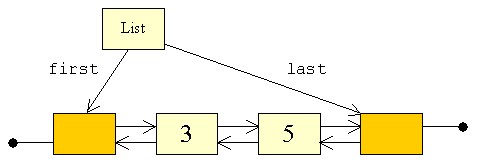
I forbindelse med testanvendelser af List-klassen, vil vi bruge instanser af java.lang.Integer, som data. Og vi vil tegne listen, ved at placere tallene i de enkelte elementer. F.eks.:

Et kald af toString, på ovenstående liste, vil returnere følgende tekststreng:

[List: 3 5]

2.2 Indsættelse

Vi vil først se på indsættelse, da det er en forudsætning for de to andre metode-grupper: søgning og sletning.

Vi skal kunne indsætte i begge ender af listen. Lad os starte forrest i listen.

2.2.1 insertFirst

Lad os først se hvordan indsættelsen skal foregå, inden vi laver implementationen.

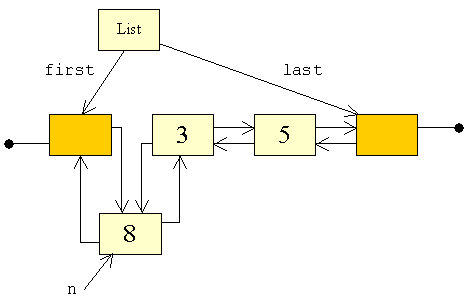
Betragt situationen i følgende figur:

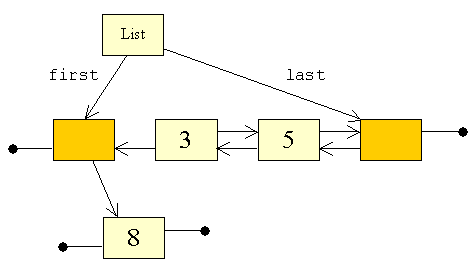
Vi har her en liste med 3 og 5. Vi ønsker nu at indsætte 8 forrest i listen. I figuren har vi gjort en ny knude klar, og sat data til at være 8.

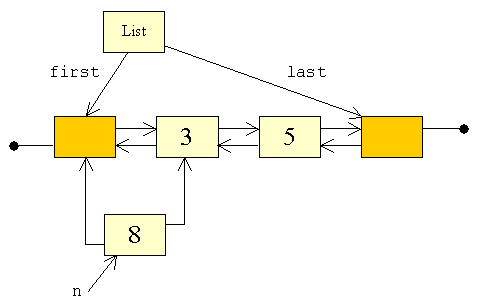
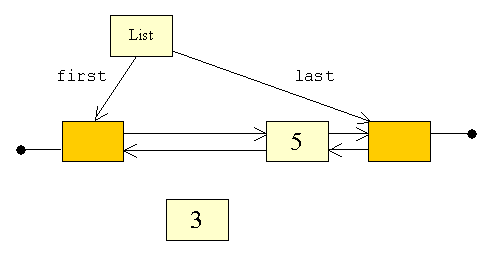
For at indsætte den nye knude mellem den forreste dummy og 3, skal vi flytte referencer. Det er i den forbindelse vigtigt ikke at miste kontakten til nogen af knuderne. Hvis vi f.eks. startede med at flytte den forreste dummy's next ville det gå galt:

Vi har mistet kontakten til 3, og dens prev kan nu kun sættes ved at vi starter ved den sidste dummy og arbejde os tilbage i listen; hvilket er en dårlig løsning.

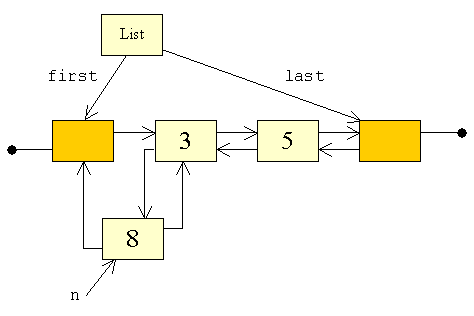
I stedet er det mere hensigtsmæssigt at starte med den nye knudes referencer - de refererer nemlig ikke til noget. Da vi har en konstruktor til Node-klassen, der kan sætte disse to referencer med det samme, er det mest bekvemt at sætte dem ved instantieringen:

List.java

public void insertFirst( Object data ) {
  Node n = new Node( data, first, first.next );

  //...
}

I figuren får vi følgende resultat:

I forbindelse med de sidste to referencer, der skal flyttes, har vi mulighed for at tage udgangspunkt i n eller first. Vi vælger at arbejde ud fra first, da det intuitivt passer bedst til det, det hele drejer sig om - nemlig indsættelse først i en liste.

List.java

public void insertFirst( Object data ) {
  Node n = new Node( data, first, first.next );
  first.next.prev = n;
  first.next = n;
  
  size++;
}

Her vælger vi, i den blå linie, først at sætte knude 3's prev (first.next.prev), da vi ellers ville miste den korte forbindelse til knude 3 (eller vi alternativt måtte flytte den sidste reference via n):

Endelig flytter vi, i den røde linie, den sidste reference:

Vi har nu fuldført operationen - knude 8, er placeret som det første element i listen.

2.2.2 insertLast

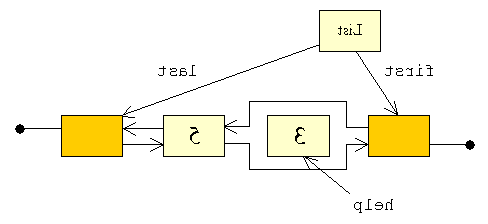
Vi vil dernæst se hvordan vi kan indsætte i slutningen af listen. Lad os se ovenstående figur "fra bagsiden".

Man skal ikke betragte ovenstående særlig længe, før man finder symmetrien slående. At indsætte i slutningen, henholdsvis starten, af listen er to fuldt ud symmetriske operationer, og dette genspejles konsekvent i implementationen:

List.java

public void insertLast( Object data ) {
  Node n = new Node( data, last.prev, last );
  last.prev.next = n;
  last.prev = n;
  
  size++;
}

Hvis man sammeligner med implementationen af insertFirst, vil man bemærke, at alle forekomster af prev og next er udskiftet med hinanden, og at first nu i stedet er last. Det er en ren "spejl-implementation"!

2.3 Sletning

I forbindelse med sletning, vil vi også fokusere på de to ender af listen, idet vi vil implementere metoderne: removeFirst og removeLast.

2.3.1 removeFirst

Formålet med denne metode, er at fjerne det forreste element i listen og efterfølgende at returnere dets data-objekt.

Hvis vi igen har følgende listen:

skal vi altså fjerne knude 3, og returnere Integer-wrapperen med værdien 3.

I den forbindelse skal vi igen være opmærksom på at holde kontakten til alle knuderne. Det nytter ikke noget at vi fjerner knude 3, hvis vi ikke holder kontakt med den:

Her har vi nok fjernet knude 3 fra listen, men vi kan ikke returnere indholdet af den fjernede knude, fordi vi ikke længere har kontakt med den!

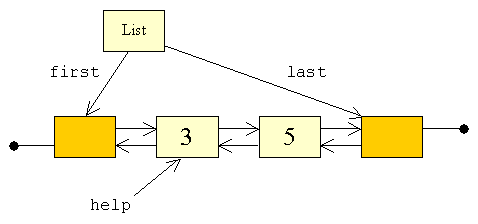
For at undgå dette, har vi brug for en midlertidig hjælp-reference: help, til at holde den knude, der skal slettes:

Da det ikke er nødvendigt at ændre prev og next på den knude vi fjerner (den skal jo alligevel ikke bruges mere), er vi ikke i yderligere fare for at miste kontakten til knuderne, og sletningen er derfor uproblematisk, idet vi blot flytter prev og next i de to nabo-knuder:

Implementationen bliver:

List.java

public Object removeFirst() {
  if ( !empty() ) {
    Node help = first.next;
    help.next.prev = first;
    first.next = help.next;
    size--;
    return help.getData();
  } else
    return null;
}

Vi har her med blåt markeret de to linier, der flytter de nævnte prev og next.

Man bemærker, at vi med size tester om der er elementer i listen, før vi begynder at fjerne det første element. Vi husker ligeledes at opdatere size efter endt sletning.

Endelig bemærker man, at vi ikke returnerer en reference til den fjernede knude, men til dens data.

2.3.2 removeLast

Vores betragtninger ovenfor, vedrørende symmetrien i insertFirst og insertLast; gør sig tilsvarende gældende for removeFirst og removeLast.

Derfor følger implementationen af simpel ombytning af first/last og prev/next.

List.java

public Object removeLast() {
  if ( !empty() ) {
    Node help = last.prev;
    help.prev.next = last;
    last.prev = help.prev;
    size--;
    return help.getData();
  } else
    return null;
}

2.4 Søgning

I forbindelse med en søgning, kan vi ønske at gøre forskellige ting ved det element vi søger efter. Først og fremmest kan vi ønske at fastslå om et element overhovedet eksisterer i containeren:

boolean exists( Object data )

Dernæst kan vi ønske at få adgang til det pågældende element:

Object find( Object data )

equals-
metoden

Umiddelbart kan man måske undre sig over hvorfor man ønsker at få adgang til noget man tilsyneladende allerede har angivet som parameter - man har jo allerede data-objektet! Forklaringen skal findes i, at vi ved søgning baserer lighed på equals-metoden, og denne kan være implementeret således, at den reelt kun sammenligner en del af data-objektets datakerne for at kunne erklære lighed. Det svarer på sin vis, til at man søger i et kartotek, og kun sammenligner med f.eks. navn og adresse. Når man finder et kartotekskort hvor disse oplysninger stemmer med søgekriteriet, tager vi kortet ud, og betragter de øvrige oplysninger på kortet.

Endelig kan man ønske at slette det søgte element:

boolean remove( Object data )

Vi har valgt at tage denne metode med under søgning, da dens implementation har større lighed med søge-metoderne, end med slette-metoderne i forrige afsnit.

Service-metode

Grunden til, at vi introducerer disse tre metoderne før deres implementation, er at de alle kan have glæde af en fælles service-metode, der finder den knude, der indeholder de søgte data.

Den fælles service-metode er:

List.java

private Node findNodeByData( Object data ) {
  for ( Node n=first.next; n!=last; n = n.next )
    if ( n.getData().equals( data ) )
      return n;

  return null;  
}

for-
løkken

for-løkken starter med det første element og itererer igennem listen. for-løkken terminerer, når den når den sidste dummy, eller når den finder en knude; hvor data-objektet er det søgte. Hvis det søgte element ikke findes i listen returneres null. Bemærk, at det her er knuden der returneres - ikke data-objektet.

2.4.1 exists

Når vi skal fastslå om der eksisterer en knude med det søgte data-objekt, er opgaven meget enkel, når vi anvender service-metoden: findNode:

List.java

public boolean exists( Object data ) {
  return findNodeByData( data ) != null;
}

2.4.2 find

Med service-metoden: findNode, er find-metoden næsten lige så enkel at implementere:

List.java

public Object find( Object data ) {
  Node n = findNodeByData( data );
    
  if ( n != null )
    return n.getData();
  else
    return null;
}

Det eneste der komplicerer den lidt, er den situation hvor det søgte element ikke findes i listen. Ellers kunne vi have klaret det med:

List.java

public Object find( Object data ) {
  return findNodeByData( data ).getData();
}

men det vil naturligvis give en NullPointerException, såfremt findNode ikke finder det søgte element.

2.4.3 remove

remove-metoden er til gengæld lidt mere interessant:

List.java

public Object remove( Object data ) {
  Node n = findNodeByData( data );
    
  if ( n != null ) {
    n.prev.next = n.next;
    n.next.prev = n.prev;
    size--;
    return n.getData();
  } else
    return null;
}

Vi har igen (med reference til removeFirst/Last) brug for en hjælpe-reference. Denne reference sættes til den reference som findNode returnerer. Såfremt denne refererer til en knude, fjerner vi knuden på sædvanlig vis, og returnerer data-objektet fra den fjernede knude.

2.5 Testanvendelse

Endelig laver vi en testanvendelse der kalder en række af metoderne:

Main.java

public class Main {

  public static void main( String[] argv ) {
    List list = new List();
    
    for ( int i=0; i<5; i++ )
      list.insertLast( i );
      
    System.out.println( list );
    
    System.out.println( list.remove( 3 ) );
    
    while ( list.size() > 0 ) {
      System.out.println( list.removeFirst() );
      System.out.println( list );
    }
  }
}

[List: 0 1 2 3 4]
3
0
[List: 1 2 4]
1
[List: 2 4]
2
[List: 4]
4
[List:]

3. SortedList-klassen

Comparable

Efter at have lavet en almindelig dobbelthægtet liste, vil vi nu se hvordan man kan holde en sådan liste sorteret. Vi vil basere ordningen af elementerne på compareTo-metoden for data-objekterne, og holde elementerne sorteret i ikke-aftagende orden. Vi kræver derfor at data-objekter implementerer Comparable-interfacet, og ændrer Node-klassen, så data-objektet skal være et Comparable-objekt. For at kunne skelne de to Node-klasser fra hinanden vælger vi samtidig at kalde den nye Node-klasse: SortedNode.

Da f.eks. insertFirst/Last-metoderne ikke giver mening i en klasse, der holderne elementerne sorteret, vil vi lave en ny klasse: SortedList. Vi vil dog genbruge store dele af List-klassen, idet følgende metoder:

Comparable removeFirst()
Comparable removeLast()
boolean exists( Comparable data )
Comparable find( Comparable data )
Comparable remove( Comparable data )
int size()
boolean empty()

i deres implementation, er helt identisk med List-klassen (Pånær at alle forekomster af Object er udskiftet med Comparable (da data-objektet nu skal være Comparable), og alle forekomster af Node er udskiftet med SortedNode). Ud over dette, genbruger vi også konstruktoren, der etablerer en tom liste.

3.1 insert

Eftersom vi skal bevare ordningen i listen hver gang vi indsætter, er det naturligt nok i forbindelse med insert-metoden, vi finder en af de væsentlige forskelle fra List-klassen. I SortedList-klassen giver insertFirst/Last ikke mening, da det alene er ordningen, der dikterer hvor et element skal indsættes.

Idéen i implementationen af insert-metoden, er at spole frem til det sted, hvor det nye element passer ind i rækkefølgen:

SortedList.java

public void insert( Comparable data ) {
  SortedNode n;
  for ( n=first.next; n!=last; n=n.next )
    if ( n.getData().compareTo( data ) >= 0 )
      break;
    
  // inds�tte f�r n
  SortedNode ny = new SortedNode( data, n.prev, n );
  n.prev = ny;
  ny.prev.next = ny;
}

Man bemærker at vi nødvendigvis må erklære n udenfor for-løkken, da den skal kunne anvendes efter løkken er termineret. Man bemærker samtidig, at det er uvæsentligt hvordan for-løkken terminerer - hvis vi ikke finder et element, der er større end det vi ønsker at indsætte, skal det netop placeres før den sidste dummy (last).

Vi laver en testanvendelse, der viser hvordan en række tilfældige elementer ordnes ved indsættelse:

Main.java

public class Main {

  public static void main( String[] argv ) {
    SortedList list = new SortedList();
    
    list.insert( 4 );
    list.insert( 5 );
    list.insert( 2 );
    list.insert( 1 );
    list.insert( 3 );
    
    System.out.println( list );
  }
}

[List: 1 2 3 4 5]

3.2 exists/find/remove

Vi har ovenfor anført disse tre metoder, blandt de metoder vi fuldt ud genbruger. Det skyldes, at de udnytter ordning af listen gennem kaldet af findNode. Det er findNode der foretager søgningen, og når det søgte elementet er fundet, er det videre forløb det samme som for List-klassen. Vi skal derfor udelukkende lave en ny implementation af findNode-metoden.

SortedList.java

private SortedNode findNode( Comparable data ) {
  SortedNode n;
  for ( n=first.next; n!=last; n=n.next )
    if ( n.getData().compareTo( data ) >= 0 )
      break;
  
  if ( n==last || n.getData().compareTo( data ) != 0 )
    return null;  
  else
    return n;
}

Man bemærker, at første del af metoden er identisk med starten af insert-metoden. Det skyldes, at der i begge tilfælde er tale om en søgning. I findNode søger vi efter et eksakt match, mens vi i insert blot søger efter, hvor elementet hører hjemme.

3.3 Fletning

Har man to instanser af SortedList, kan man flette dem, som det kendes fra flette-sortering.

Ved en fletning af to lister, kan man lave en tredie. Vi vil derfor lave en konstruktor, der tager to instanser af SortedList som parametre, og foretager en fletning, idet knuderne fra de to lister placeres i den nye liste. Det betyder, at de oprindelige lister vil blive tømt for knuder, og efterfølgende er tomme lister (man kunne alternativt vælge at implementere konstruktoren, så den i stedet kopierede de enkelte elementer, og lod de oprindelige lister være uberørte).

SortedList.java

public SortedList( SortedList list1, SortedList list2 ) {
  this(); // etablerer den tomme liste
  SortedNode p1 = list1.first.next;
  SortedNode p2 = list2.first.next;
  
  while ( p1 != list1.last && p2 != list2.last ) {
    // stadig elementer i begge lister
    
    if ( p1.getData().compareTo( p2.getData() ) < 0 )
      // p1's er mindst
      p1 = insertNodeLast( p1 );
    else if ( p1.getData().compareTo( p2.getData() ) > 0 )
      // p2's er mindst
      p2 = insertNodeLast( p2 );
    else {
      // p1 pg p2 er lige store
      p1 = insertNodeLast( p1 );
      p2 = insertNodeLast( p2 );
    }
  }
  
  while ( p1 != list1.last )
    // der er flere tilbage i list1
    p1 = insertNodeLast( p1 );
  
  while ( p2 != list2.last )
    // der er flere tilbage i list2
    p2 = insertNodeLast( p2 );
  
  list1.clear();
  list2.clear();
}

Metoden tager elementerne fra de to oprindelige lister, uden hensyntagen til disses interne integritet, og de kommer derfor til ikke at "hænger sammen". Der afsluttes derfor med et kald af clear-metoden:

SortedList.java

public void clear() {
  first.next = last;
  last.prev = first;

  size = 0;
}

der initialiserer listerne til at være tomme. Denne metode kan også kaldes fra default-konstruktoren, da denne slutter med at gøre det samme, efter at have instantieret de to dummies.

insertNodeLast indsætter en "stjålen" knude sidst i listen, og returnerer en reference til den knude der før indsættelsen kom efter den "stjålne" knude:

SortedList.java

private SortedNode insertNodeLast( SortedNode node ) {
  SortedNode nextNode = node.next;
    
  node.next = last;
  node.prev = last.prev;
    
  node.prev.next = node;
  node.next.prev = node;
    
  return nextNode;
}

At efterfølgeren returneres af metoden, gør det muligt at vandre videre henad den pågældende liste, selvom den er ved at blive "trevlet op".