© 1999-2003, Flemming Koch Jensen Alle rettigheder forbeholdt

Iteration Opgaver

"..." - ...

Abstract: Gennemgår iteration med arrays som den grundlæggende motivation. Først gennemgås en-dimensionelle arrays, mens fler-dimensionelle arrays venter til efter de iterative kontrolstrukturer er introduceret. do-while præsenteres som en variant af while, og for-sætningen som et specialtilfælde af while. break og continue gennemgås, og muligheden for at anvende labels. I forbindelse med fler-dimensionelle arrays introduceres asymmetriske arrays.

Forudsætninger: Kendskab til if-sætningen og boolske udtryk.

 

 

Iteration er gentagelse	I kapitlet om algoritmer var der et eksempel på en gentagelse: "Så længe det brænder så smid vand på ilden". Gentagelse er den anden gruppe af kontrolstrukturer vi skal studere. Fagudtrykket for gentagelse er iteration, og sammen med selektion beskriver de, de muligheder vi har for at kontrollere/bestemme hvilke sætninger der skal udføres. For iteration er det ikke så meget et spørgsmål om en sætning skal udføres, men om hvor mange gange den skal udføres. Det kan naturligvis også dreje sig om nul eller én gang, som er mulighederne for if-sætningen.
	Inden vi ser på den første iterative kontrolstruktur skal vi omkring en datastruktur der er tæt knyttet til iterative algoritmer: Arrayet.
	1. Arrays
Organiserer data af samme type i tabel	Arrays bruges til at organisere data af samme type i en tabel-lignende struktur. Vi kan derfor bruge det danske ord tabel som synonym for array (eng. række). Vi vil indledningsvis indskrænke os til at se på arrays der kun indeholder én række af data, såkaldte en-dimensionelle arrays. Sådanne arrays tegner man ofte som en række af felter der hver indeholder en værdi af arrayets datatype. Et array med datatype int, kunne f.eks. have følgende udseeende.
Figur 1: Array med ti elementer
Index refererer til elementer i arrayet	Dette array har ti værdier fordelt i de ti felter. Man kalder felterne for indgange i arrayet, og værdierne for elementer. Man kunne derfor sige, at i arrayets første indgang har vi elementet 5. Eller i daglig tale, at det første element er 5. Da der er et "en til en" forhold mellem indgange og elementer bliver forskellen ofte udvandet, og man foretrække normalt at bruge betegnelsen element frem for indgang, når det er klart hvad man mener. De forskellige indgange er nummereret fra 0 og opefter. Disse numre kaldes index. Man bruger index til at referere til elementerne i arrayet, for derved at kunne arbejde med dem.
Figur 2: Array med index
Index fra 0 til n-1; hvor n er længden	Man bemærker at det største index er 9, og dermed én mindre end antallet af elementer i arrayet. Det er en sammenhæng der er nyttig at huske: index går fra 0 til n-1; hvor n er antallet af elementer. Antallet af elementer betegnes også som arrayets længde.
	1.1 Erklæring af arrays
	Hvordan erklærer man et array?
	Lad os se hvordan man kunne erklære arrayet ovenfor med de ti elementer.
Source 1: Erklæring med initialisering	int[] vorTabel = { 5, 3, -2, 9, 0, -5, 10, 11, -7, 10 };
Man kan kun bruge en initialiserings-liste i erklæringen	Først har vi arrayets type: int, efterfulgt af []. [ og ] kaldes kantede paranteser. Ved at placere disse efter typen angiver vi at der er tale om et array af int. Dernæst følger navnet på arrayet. Som enhver anden variabel skal arrayet have et navn så vi kan referere til det. Efter navnet følger et lighedstegn, der har samme effekt som et assignment. Man skal dog bemærke at denne form for assignment kun kan forekomme i erklæringen. Det specielle ved højresiden af dette assignment er at der optræder en række af tal, som skal være elementer i arrayet. Elementerne er adskilt med komma og samlet med tuborg-paranteser. Endelig er erklæringen, som enhver anden sætning, afsluttet med semikolon.
	1.2 Anvendelse af arrays
	Nu har vi et array, men hvordan anvendes det?
	Som tidligere nævnt bruger man index som reference til de enkelte elementer. Rent syntaktisk refererer man til elementer med følgende konstruktion:
Syntax 1: Reference til element	<array-navn> [ <index> ]
De kantede paranteser er arrays varemærke	Først er der navnet på arrayet, dernæst følger index i kantede paranteser. Man bemærker at de kantede paranteser går igen fra erklæringen, og de er da også arrays syntaktiske varemærke, der tydeligt adskiller dem fra alt andet.
	Vi kunne f.eks. udskrive nogle vilkårlige elementer fra vores array med:
Source 2: Udskrift af fire elementer	System.out.println( vorTabel[0] ); System.out.println( vorTabel[3] ); System.out.println( vorTabel[4] ); System.out.println( vorTabel[9] ); 5 9 0 10
Kontruktionen med kantede paranteser er som et variabelnavn	Som man ser, optræder konstruktionen med de kantede paranteser, ligesom et variabelnavn. Det er også tilfældet i enhver anden sammenhæng. F.eks. kunne vi hente en værdi fra arrayet og lægge den over i en almindelig variabel af typen int:
Source 3: Hente værdi fra array	int x; x = vorTabel[8]; x = x + 5; System.out.println( x ); -2
	Her beregnes -7+5 = -2, som udskrives. Da referencen til et element i et array fungerer ligesom enhver anden variabel, kunne vi også have valgt at gøre det samme med:
Source 4: Reference i udtryk	int x; x = vorTabel[8] + 5; System.out.println( x );
	eller i ét "hug":
Source 5: Reference i udtryk	System.out.println( vorTabel[8] + 5 );
	Vi kan ligeledes ændre værdierne i arrayet med assignments:
Source 6: Ændring af værdier i array	vorTabel[6] = 3; vorTabel[7] = 3; System.out.println( vorTabel[6] ); System.out.println( vorTabel[6]==vorTabel[7] ); 3 true
	Som det ses, kan konstruktionen med kantede paranteser bruges fuldstændig som ethvert andet variabelnavn.
	Index behøver ikke være et literale, det kan også være et numerisk udtryk. F.eks.
Source 7: Index som numerisk udtryk	int x=0; System.out.println( vorTabel[x] ); System.out.println( vorTabel[x+1] ); System.out.println( vorTabel[x+2] ); 5 3 -2
	hvor de første tre elementer i arrayet udskrives.
	1.3 Allokering af arrays
Erklære og senere indsætte værdier	Da vi erklærede arrayet, angav vi nogle værdier det skulle initialiseres til at indeholde. Men, som vi så ovenfor, kan man senere tildele de forskellige indgange nye værdier. Man kan derfor have behov for at erklære arrays af en vis størrelse, for først senere at tildele indgangene værdier.
	Vores array med ti indgange kunne være erklæret ved:
Source 8: Erklæring med allokering	int[] vorTabel = new int[10];
Allokering er reservering af plads i lagret	Det ville bevirke at et tomt array med ti indgange blev allokeret. Man kalder det allokering når der i lagret reserveres plads til noget, i dette tilfælde et array. I særdeleshed kalder vi det allokering når vi selv bevidst forårsager dette. Højresiden af assignment har en angivelse med new, der udtrykker at vi ønsker, at der skal allokeres et område i lagret med den beskaffenhed der efterfølgende er angivet. Denne angivelse lyder på 10 pladser til data af typen int.
Default er 0 for alle indgange	Som udgangspunkt har indgangene i det nye array ingen værdi, for vi har ikke angivet nogen. Det er dog sådan, i java, at et nyt array uden værdier default har værdien 0 i alle indgange, så de er ikke udefinerede. Hvis vi efterfølgende skulle initialisere arrayet, måtte det nu gøres med ti assignments:
Source 9: Initialisering med assignments	vorTabel[0] = 5; vorTabel[1] = 3; vorTabel[2] = -2; vorTabel[3] = 9; vorTabel[4] = 0; vorTabel[5] = -5; vorTabel[6] = 10; vorTabel[7] = 11; vorTabel[8] = -7; vorTabel[9] = 10;
	Det er naturligvis meget omstændeligt at initialisere et array på denne måde; hvorfor erklæring med samtidig initialisering er at foretrække når vi alligevel vil have en sådan.
Arrays kan ikke ændre størrelse	Inden vi går videre med iterativ anvendelse af arrays er der endnu en egenskab vi skal bemærke: Et array kan ikke ændre størrelse! Når det først er allokeret kan man hverken øge eller mindske antallet af indgange. Dette betegner man som en statisk egenskab ved arrays. Statisk, fordi det ikke kan ændre sig under programudførelsen.
Længde af array	Det er muligt at finde længden af et array, uden at skulle anføre det som et literale. Det gøres ved at skrive arrayets navn efterfulgt af ordet length, adskilt med punktum. F.eks.
Source 10: Et arrays længde	System.out.println( vorTabel.length ); 10
Brug aldrig et literale	Det er altid at foretrække, at man bruger denne notation i stedet for at anføre arrayets længde som et literale. Det skyldes, at man dermed ikke skal ændre det pågældende sted i programmet, hvis man senere compilerer det med en anden længde på arrayet.
	2. while-sætningen
	Lad os fortsat arbejde med vores array med de ti elementer. Hvordan kan vi udregne summen af elementerne i arrayet? Det kunne gøres på følgende måde:
Source 11: Sum af elementer	int sum=0; sum += vorTabel[0]; sum += vorTabel[1]; sum += vorTabel[2]; sum += vorTabel[3]; sum += vorTabel[4]; sum += vorTabel[5]; sum += vorTabel[6]; sum += vorTabel[7]; sum += vorTabel[8]; sum += vorTabel[9]; System.out.println( sum ); 34
Gentagende mønster	Her kunne den første linie; hvor sum initialiseres til 0, naturligvis fjernes, hvis man i stedet initialiserede den til vorTabel[0] i næste linie. Dette er ikke gjort, da det ensartede mønster i de ti adderende assignments er centralt i vort videre ræsonnement.
	Man bemærker at index udvikler sig fra 0 og bliver en større for hver gang vi tilgår et element i arrayet. Vi kan udvikle denne sammenhæng ved at indføre en variabel index, der gennemløber disse værdier.
Source 12: Med index-variabel	int sum=0; int index=0; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; sum += vorTabel[index]; index++; System.out.println( sum );
To linier gentages ti gange	Igen kunne vi her have sparet en linie, nemlig den sidste index++. Igen har vi valgt at tage den med for at understrege det gentagende mønster i forløbet. Der findes nu kun fire forskellige linier, hvoraf de sidste to er gentaget ti gange. Det der er afgørende for hvor mange gange disse to linier gentages er antallet af gange vi har skrevet dem. Det er statisk fastlagt. Hvis vi på anden måde skulle styre antallet af gange linierne udføres, burde de derfor ikke skulle gentages rent tekstuelt, men blot stå der én gang.
Pseudo 1: Gentag ti gange	int sum=0; int index=0; // De næste to linier skal udføres ti gange sum += vorTabel[index]; index++;
Hvad der betinger gentagelsen	Som kommentarens manglende virkning på programudførelsen illustrerer, har vi brug for hjælp. Hjælpen kommer fra while-sætningen. For at kunne anvende denne hjælp må vi dog først gå fra at fokusere på hvor mange gange det skal gentages til at beskrive hvad der betinger at det skal gentages. Her er index-variabelen nøglen. Den inkrementeres løbende og dens størrelse kan danne grundlag for styring af gentagelsen. Index må naturligvis ikke vokse i det uendelige. I vores eksempel må den ikke blive større end index for det sidste element i arrayet, nemlig 9. Vi kan derfor udvikle kommentaren ovenfor, og få følgende:
Pseudo 2: Så længe	int sum=0; int index=0; // Så længe index<10 så udfør de næste to linier sum += vorTabel[index]; index++;
while = "Så længe"	Det er stadig kun en effektløs kommentar, men vi er nu kun et lille skridt fra at anvende while-sætningen, der har samme virkning som "så længe".
Source 13: Sum med while-sætning	int sum=0; int index=0; while ( index < 10 ) { sum += vorTabel[index]; index++; }
Syntaktisk lighed med if-sætningen	Først bemærker man den syntaktiske lighed med if-sætningen. Den eneste forskel er ordet while i stedet for if, ellers er udseendet det samme: paranteser omkring udtrykket, der kaldes kørselsbetingelsen, og brug af en sammensat sætning hvis der skal kontrolleres mere end én sætning.
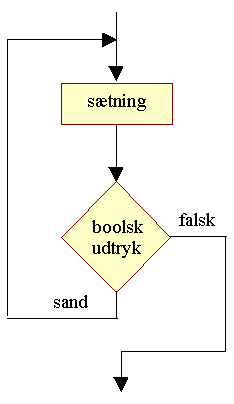
	Den syntaktiske lighed med if-sætningen understreges af dataflow-diagrammet for while-sætningen.
Figur 3: Dataflow-diagram for while-sætningen
Cirkulær bevægelse kaldes løkke	Hvis man sammenligner med det tilsvarende dataflow-diagram for if-sætningen er forskellen minimal. Mere præcist ligger forskellen i, at efter sætningen er udført går while-sætningen tilbage og re-evaluerer kørselsbetingelsen, mens if-sætningen blot fortsætter udførelsen efter if-sætningen. Det er den cirkulære bevægelse i while-sætningens dataflow-diagram, der har givet den navnet while-løkken. Man kan derfor betegne while-sætningen som en gentagende if-sætning.
	Lad os se nogle eksempler på simple while-sætninger. Vi vil først bevæge os lidt væk fra arrays for at starte så simpelt som muligt.
Source 14: Sum af de første ti heltal1	Eksempel: Beregn 1 + 2 + ... + 10 int sum=0; int tal=1; while ( tal <= 10 ) { sum += tal; tal++; } System.out.println( sum ); 55
Læsbarhed vigtigt	Man bemærker, at vi har valgt kørselsbetingelsen tal<=10 frem for tal<11, da 10 bedre udtrykker at vi beregner summen fra 1 til 10, mens det ville være mere uklart med 11.
Source 15: Tre-tabellen	Eksempel: Udskriv tre-tabellen int tal=3; while ( tal <= 10*3 ) { System.out.println( tal ); tal += 3; } 3 6 9 12 15 18 21 24 27 30
Compileren beregner konstante udtryk	Her bemærker vi to ting. Først og fremmest tæller vi nu tal op med 3, men også i kørselsbetingelsen optræder 3. Vi vælger nemlig at skrive 10*3, fordi det bedre signalerer til læseren, at der er tale om tre-tabellen, frem for 30 der ville fortælle mindre. Man skal ikke bekymre sig mht. effektiviteten, compileren erstatter de 10*3 med 30 når den oversætter og det bliver derfor ikke beregnet hver gang udtrykket evalueres.
Source 16: Tre i femte	Eksempel: Beregn 35 int produkt=1; int gange=1; while ( gange <= 5 ) { produkt *= 3; gange++; } System.out.println( produkt ); 243
	2.1 Neutral-element
Neutral-element har ingen effekt	Inden vi vender tilbage til iteration over arrays skal vi gøre en observation. Vi har flere gange itereret i forbindelse med summering. I de situationer har vi initialiseret vores variabel til 0. Da vi i det sidste eksempel ovenfor havde brug for at initialisere produkt med noget der ligeledes var uden effekt, valgte vi 1. Dette at 0 ikke har nogen effekt i forbindelse med addition og 1 har den tilsvarende egenskab for multiplikation, benævner man at 0 er neutral-element for plus og 1 er neutral-element for gange.
	Neutral-elementet for en operator kan defineres ved:
	Definition: Neutral-element Neutral-elementet for en operator er det element e for hvilket der gælder: e <operator> x = x for alle x.
	I eksemplet med tre i femte kunne vi alternativt starte med værdien 3:
Source 17: Starte med 3	int produkt=3; int gange=1; while ( gange <= 4 ) { produkt *= 3; gange++; }
Neutral-element gør det mere læsbart	Det er mere stilrent at starte med 1, fordi det er neutral-element. Ligeledes fordi tallet 5 nu er ændret til 4, der ikke umiddelbart har nogen sammenhæng med 35 - altså mindre læsbarhed. Alternativt kunne man bruge udtrykket gange<5, men at vi ikke må nå 5, er stadig mindre læsbart.
	2.2 Iteration over arrays
	Lad os vende tilbage til en række eksempler, denne gang med arrays. Vi vil fortsat tage udgangspunkt i vores array med de ti elementer.
Source 18: Sum af positive elementer	Eksempel: Summen af de positive elementer i et array int sum=0; int index=0; while ( index < vorTabel.length ) { if ( vorTabel[index] > 0 ) sum += vorTabel[index]; index++; } System.out.println( sum ); 48
	Her lader vi en if-sætning styre at kun de positive værdier summeres.
	Man bemærker, at vi her bruger arrayets længde i kørselsbetingelsen, og ikke direkte anfører længden 10. Det gør programmet lettere at læse, da det relativt anonyme 10 nu er erstattet med den mere sigende længdeangivelse.
Source 19: Inkrementering af alle elementer	Eksempel: Inkrementer alle elementer (dvs. tæl alle elementer op med én) int index=0; while ( index < vorTabel.length ) { vorTabel[index]++; index++; }
	Eksemplet understreger, at konstruktionen med de kantede paranteser syntaktisk kan anvendes helt på lige fod med et variabel-navn. Det betyder her, at efterstillet ++ inkrementerer det element i arrayet, der refereres til.
	3. do-while-sætningen
Variant af while-sætningen	do-while-sætningen er en variant af while-sætningen. Med while-sætningen kan man foretage 0 til flere iterationer, idet vi allerede før den første iteration foretager en kørselskontrol. Sekvensen af iterationer, og evaluering af kørselsbetingelsen, er derfor:
Pseudo 3: while-forløbet	Evaluer kørselsbetingelsen Udfør sætningen Evaluer kørselsbetingelsen ... Udfør sætningen Evaluer kørselsbetingelsen
	Man bemærker at der altid afsluttes med en evaluering af kørselsbetingelsen, nemlig den der konstaterer at der ikke skal itereres mere.
	do-while varianten har følgende forløb:
Pseudo 4: do-while-forløbet	Udfør sætningen Evaluer kørselsbetingelsen Udfør sætningen ... Udfør sætningen Evaluer kørselsbetingelsen
Sætning udføres mindst én gang	Som man ser, er den eneste forskel at sætningen udføres første gang uden nogen indledende kontrol af kørselsbetingelsen. Forskellen er meget lille og do-while-sætningens bidrag er heller ikke den store fornyelse.
	do-while-sætningen anvendes naturligvis i de situationer, hvor man vil sikre sig at sætningen bliver udført mindst én gang. Det kan f.eks. være situationer hvor det ikke giver mening at evaluere kørselsbetingelsen før sætningen har tildelt visse variable en værdi - variable som indgår i kørselsbetingelsen.
	Syntaksen for do-while-sætningen er en del anderledes end if- og while-sætningen.
Syntax 2: do-while	do {   <sætninger> } while ( <boolsk udtryk> );
	Tuborg paranteserne skal anvendes; hvis der er mere end én sætning - ellers er de ikke nødvendige.
Evaluering af kørsels-betingelsen efter iteration	Som man ser er kørselsbetingelsen flyttet ned efter iterationen, hvilket illustrerer at den først evalueres efter hver iteration. At evalueringen  sker efter hver iteration, har kun reel betydning for første iteration. Det skyldes at alle efterfølgende evalueringer alligevel ligger mellem iterationer, pånær den sidste naturligvis.
	Ligheden mellem while- og do-while-sætningen ses også af deres dataflow-diagrammer. Dataflow-diagrammet for do-while har følgende udseende:
Figur 4: dataflow-diagrammet for do-while
	I forhold til while er sætningen blot flyttet op foran, mens sand stadig fører til iteration af sætningen og falsk terminerer strukturen.
Source 20: Største tal der ganget med 7 er mindre end 100	Eksempel: Find det største tal der ganget med 7 er mindre end 100 int tal=0; int sum=0; do { sum += 7; tal++; } while ( sum<100 ); System.out.println( tal-1 ); 14
	14*7 = 98, og 14 er dermed det største tal man kan gange med 7 så det er mindre end 100.
Kunne have brugt while	Man bemærker at kørselsbetingelsen godt kunne have været evalueret før første iteration, samt at dette stadig ville have bevirket at iterationen blev udført. Derfor har det i denne situation ingen betydning, at vi har valgt en do-while i stedet for en while. Forskellen kommer kun til sin ret, hvis kørselsbetingelsen ikke er opfyldt første gang (eller ikke kan evalueres første gang).
Source 21: Indlæsning af talfølge fra brugeren	Eksempel: Indlæs talfølge og udskriv summen BufferedReader indlæser = new BufferedReader( new InputStreamReader( System.in ) ); int sum=0; int tal; do { System.out.print( "Indtast tal: " ); tal = Integer.parseInt( indlæser.readLine() ); sum += tal; } while ( tal!=0 ); System.out.println( "Summen er " + sum ); Indtast tal: 5 Indtast tal: 10 Indtast tal: -3 Indtast tal: 2 Indtast tal: 0 Summen er 14
	Her vil kørselsbetingelsen ikke give mening før iterationen har kørt første gang. Variabelen tal vil være udefineret inden den i første iteration får en værdi. En while-version ville derfor ikke kunne anvendes.
	3.1 Er do-while nødvendig?
do-while er ikke nødvendig	Rent sprog-teoretisk kunne man spørge om do-while er en nødvendighed - er der algoritmer vi ikke kan formulere uden do-while? Svaret er nej! Enhver do-while kan laves ved anvendelse af en while.
	Hvis vi betragter den grundlæggende syntaks for do-while
Syntax 3: do-while-sætningen	do {   <sætninger> } while ( <kørselsbetingelse> );
	kan det tilsvarende laves med følgende anvendelse af while-sætningen:
Syntax 4: while-version af do-while	<sætninger> while ( <kørselsbetingelse> ) { <sætninger> }
	Man vil være nød til at gentage de samme sætninger før selve while-sætningen for at opnå den indledende udførelse af disse. Man bemærker at kørselsbetingelsen vil være uforandret.
	4. for-sætningen
	for-sætningen er syntaktisk sukker for en bestemt anvendelse af while-sætningen. Vi vil i den forbindelse opdele iteration i to grupper: tæller-styret og sentinel-styret.
	4.1 Tællerstyret iteration
Tæller-variabel	Tællerstyret iteration styres af en tæller-variabel. En tællervariabel er en numerisk variabel der gennemløber en række værdier og terminerer løkken når en grænseværdi er nået. F.eks.:
Source 22: Udskriv array	Eksempel: Udskriv array int tæller=0; while ( tæller<vorTabel.length ) { System.out.print( vorTabel[tæller] + " " ); tæller++; } System.out.println(); 5 3 -2 9 0 -5 10 11 -7 10
	Vi kan her identificere tre elementer der styrer løkkens forløb.
	Først er der initialiseringen af tælleren. I vores eksempel er startværdien 0, men den kunne naturligvis have været et vilkårligt heltal.
	Dernæst er der grænseværdien. I vores eksempel er den 10, idet vorTabel.length er 10. Tælleren vil bevæge sig fra startværdien mod grænseværdien efterhånden som løkken kører.
	Endelig er der ændringen af tælleren. I vores eksempel tælles den op med én, men springet kunne naturligvis være større, som det ses i følgende eksempel:
Source 23: De lige tal fra 0 til 10	Eksempel: Udskriv de lige tal fra 0 til 10 int tal=0; while ( tal<=10 ) { System.out.print( tal + " " ); tal += 2; } System.out.println(); 0 2 4 6 8 10
	Her ændres tælleren hver gang med 2, og vi får behændigt udskrevet de lige tal, ved at springe de ulige over.
	De tre algoritmiske elementer: initialisering, check af grænseværdi og ændring er karakteristiske for mange anvendelser af while-sætningen. Man har derfor lavet en syntaktisk struktur der understøtter forståelsen af disse tre elementer. Det er for-sætningen.
	Lad os se ovenstående eksempel med anvendelse af for-sætningen:
Source 24: De lige tal med for-sætning	for ( int tal=0; tal<=10; tal+=2 ) System.out.print( tal + " " ); System.out.println();
	Som man ser er de tre algoritmiske elementer nu samlet på én linie. Det gør det hurtigt at få et indtryk af hvordan løkken forløber, men det er naturligvis kun syntaktisk sukker for den tilsvarende while-sætning.
	Den generelle syntaks for for-sætningen er:
Syntax 5: for-sætning	for ( <sætning>; <boolsk udtryk>; <sætning> )   <sætning>;
	Eller en anelse mere sigende:
Syntax 6: for-sætning	for ( <initialisering>; <kørselsbetingelse>; <ændring af tæller> ) <sætning>;
	Lad os se endnu et eksempel:
Source 25: Summen af de første ti heltal	Eksempel: Beregn 1 + 2 + ... + 10 int sum=0; for ( int tal=1; tal<=10; tal++ ) sum += tal; System.out.println( sum ); 55
	Man kan, som for de andre kontrolstrukturer, beskrive for-sætningen med et dataflow-diagram:
Figur 5: Dataflow-diagrammet for for-sætningen
	Hvis man slår Sætning og Ændring sammen er ligheden med dataflow-diagrammet for while-sætningen tydelig. Vi kan også beskrive sammenhængen i pseudo-kode:
Syntax 7: while-sætning ækvivalent med for-sætningen	<initialisering> while ( <kørselsbetingelse> ) { <sætning> <ændring af tæller> }
	for-sætningen er en bekvemmelighed, ikke kun når man programmerer med den, men også når man læser den. Når man ser den, ved man at der er tale om tællerstyret iteration og på én linie får man overblik over løkkens styring.
	4.1 Standard for-løkke
Ofte forekommende for-løkke	Ligesom for-sætningen beskriver en ellers ofte forekommende anvendelse af while-sætningen, således er der også en bestemt slags for-løkker der forekommer ofte. Det er standard for-løkken [FKJ]. Den er givet ved:
Syntax 8: standard for-løkken	for ( int <tæller>=0; <tæller> < <antal>; <tæller>++ ) <sætning>;
	<tæller> er et variabelnavn og <antal> er en fast grænseværdi.
	Standard for-løkken kører <antal> iterationer. Den anvendes primært i to situationer:
	Når man ønsker et bestemt <antal> iterationer og <tæller> anvendes ikke i <sætning>. Når man ønsker at gennemløbe et array og <antal> er længden af arrayet. <tæller> anvendes som index i arrayet.
	4.2 Sentinelstyret iteration
Sentinellen er en variabel	Sentinel betyder skildvagt, sådan en med en hellebard, der står vagt ved borgporte. Sentinellen er en variabel som styrer om løkken fortsætter eller terminerer. Vi har allerede set et eksempel på dette i afsnittet om do-while:
Source 26: Indlæsning af tal-række fra brugeren	BufferedReader indlæser = new BufferedReader( new InputStreamReader( System.in ) ); int sum=0; int tal; do { System.out.println( "Indtast tal: " ); tal = Integer.parseInt( indlæser.readLine() ); sum += tal; } while ( tal != 0 ); System.out.println( "Summen er " + sum );
Sentinel-værdien	Her er sentinellen tal, og den værdi der terminerer løkken er 0. Man kalder 0 for sentinel-værdien, da det er den værdi som sentinelvariabelen skal antage, for at sentinellen løfter hellebarden og lader os slippe ud af løkken.
	5. break og continue
break og continue virker på enhver løkke	break og continue er to primitive sætninger der kan bruges til at styre en løkkes forløb. De kan være nyttige i visse situationer, men de har en pris - de gør kildeteksten vanskeligere at læse.
	5.1 break
Ubetinget break er uanvendeligt	break afbryder udførelsen af en løkke - får den til at terminere øjeblikkeligt. break anvendes naturligvis altid i forbindelse med en if-sætning, da et ubetinget break i praksis er uanvendeligt til noget fornuftigt formål.
Source 27: Brug af break	Eksempel: Find det mindste tre-cifrede tal, der er deleligt med 7 int tal=100; while ( tal<1000 ) { if ( tal%7 == 0 ) break; tal++; } System.out.println( tal ); 105
	15*7 = 105, og 105 er derfor tallet vi søger.
Kan terminere af to grunde	Vi terminerer løkken med break når 7 går op i tal. Derfor vil tal efter løkke være den søgte værdi. I princippet kunne løkken også terminere ved at kørselsbetingelsen ikke længere var opfyldt, at tal blev fire-cifret, men da der findes en løsning, sker dette ikke.
	5.2 for-sætningens virkefelt
Erklæret i initialisering, eksisterer kun i sætningen	Variable som erklæres i initialiseringen af for-sætningen eksisterer kun i sætningens virkefelt. Det betyder at en tællervariabel ikke er tilgængelig efter for-sætningen, idet den ikke eksisterer efter løkkens terminering. Hvis man efterfølgende har brug for tælleren, må man derfor flytte selve erklæringen ud før for-sætningen. I forbindelse med anvendelser af break i for-sætninger, får man ofte brug for dette.
Source 28: Finde tal i array	Eksempel: Find et tal i et array int target=11; int index; for ( index=0; index<vorTabel.length; index++ ) if ( vorTabel[index] == target ) break; if ( index<vorTabel.length ) System.out.println( target + " er på position " + index ); else System.out.println( target + " findes ikke" ); 11 er på position 7
index fortæller indirekte om løkkens terminering	Her break'er man ud af for-løkken, hvis man finder den søgte værdi. Efter for-løkken kan man derfor bruge index's værdi som en indikator for om værdien blev fundet. Det skyldes at index indirekte fortæller hvordan løkken terminerede. Om det var fordi grænseværdien blev nået eller før.
	Generelt kan man anvende følgende skabelon i forbindelse med break løkker:
	for ( ...; <kørselsbetingelse>; ... ) { ... break; ... } if ( <kørselsbetingelse> ) // blev afbrudt else // kørte igennem
	5.3 continue
Terminerer kun iterationen	Idéen med continue er knap så drastisk som med break. I stedet for helt at terminere løkken, vil continue kun afbryde den igangværende iteration. Det betyder at løkken kan fortsætte, men at resten af løkkens indhold springes over. Med andre ord: "Drop resten af iterationen og lad os se om vi skal køre igen".
Source 29: Brug af continue	Eksempel: Udskriv de negative tal fra et array, og beregn samtidig summen af dem int sum=0; for ( int index=0; index<vorTabel.length; index++ ) { if ( vorTabel[index] >= 0 ) continue; System.out.print( vorTabel[index] + " " ); sum += vorTabel[index]; } System.out.println( "Summen er " + sum ); -2 -5 -7 Summen er -14
	Her bevirker en udførelse af continue, at de to sidste sætninger ikke udføres. Det bemærkes, at eksemplet ikke er god programmeringsskik, da det i stedet ville være enklere med en betinget udskrift og summering.
	5.4 Label'ede break og continue
	Den løkke som break og continue virker på, er som bekendt den nærmest - den inderste. I sjældne tilfælde har man brug for at break eller continue ikke vedrører den inderste løkke, men derimod en der befinder sig længere ude.
	Lad os se et eksempel. Vi ønsker at gennemløbe den lille tabel vha. to for-løkker inden i hinanden, og i den forbindelse finde to tal, der ganget med hinanden giver 42.
	Vores første forsøg kunne være følgende:
Source 30: Forgæves brug af break	Eksempel: Hvad giver 42 i den lille tabel? for ( int i=1; i<=10; i++ ) for ( int j=1; j<=10; j++ ) if ( i*j == 42 ) { System.out.println( i + "*" + j + " = " + i*j ); break; } 6*7 = 42 7*6 = 42
	Som man ser, er vores break forgæves - vi slipper kun ud af den inderste løkke.
Label'et break	Til at løse netop denne slags problemer, findes der en label'et udgave af break. Man kan ganske enkelt navngive den yderste for-løkke og dernæst anvende dette navn i forbindelse med break.
	Ved anvendelse af et label'et break bliver vores program som følger:
Source 31: Brug af label'et break	Eksempel: Hvad giver 42 i den lille tabel? ydre: for ( int i=1; i<=10; i++ ) for ( int j=1; j<=10; j++ ) if ( i*j == 42 ) { System.out.println( i + "*" + j + " = " + i*j ); break ydre; } 6*7 = 42
	Navnet anføres før den pågældende løkke med et efterfølgende kolon, og det er dette navn som betegnes: et label. Vi har her angivet navnet på samme linie som for-løkken, men det ses ofte, at man placerer det på linien før:
Source 32: Label'et break på linien før	ydre: for ( int i=1; i<=10; i++ ) for ( int j=1; j<=10; j++ ) if ( i*j == 42 ) { System.out.println( i + "*" + j + " = " + i*j ); break ydre; }
Label'et continue	Label'et continue findes fuldstændig tilsvarende, men vi vil undlade at se et eksempel, da muligheden for label'ing fungerer fuldstændig tilsvarende.
	6. Lagerforståelse af arrays
	Inden vi fortsætter vores studie af iteration skal vi udbygge vores kendskab til arrays. I første række vil det dreje sig om lagerforståelse og dernæst om fler-dimensionelle arrays.
Reserverer område i lagret	Som tidligere nævnt, i forbindelse med allokering af arrays, reserveres der et område i lageret når vi erklærer et array. Dette område er en samling af lagerceller der vil indeholde arrayets elementer.
Source 33: Reference til allokeret array	int[] vorTabel = new int[10];
vorTabel er reference til arrayet	Her reserveres plads til 10 integers og vi giver arrayet navnet vorTabel. At arrayet er en variabel, med et navn, på lige fod med andre variable er ikke helt korrekt; det er blot en bekvem måde at se det på. Det der præcist sker, er at vi laver en variabel der refererer til det område i lagret vi netop har allokeret. vorTabel er en reference vi bruger til at holde fast i arrayet, så vi efterfølgende kan arbejde med det. Lad os se et eksempel der fremhæver reference-egenskaberne ved vorTabel.
Source 34: Assignment med referencer	int[] vorTabel = new int[10]; int[] listen = vorTabel;
	Her bliver listen sat til at referere til det samme array som vorTabel refererer til. De er begge referencer til det samme område i lageret, og vi har nu to referencer vi kan bruge på lige fod i arbejdet med disse data.
Source 35: Flere referencer til samme array	int[] vorTabel = new int[10]; int[] listen = vorTabel; vorTabel[0] = 3; vorTabel[1] = 5; System.out.println( listen[0] ); System.out.println( listen[1] ); 3 5
	Vi bruger her referencen vorTabel til at lægge værdier i arrayet, og dernæst referencen listen til at tilgå disse værdier. Der er naturligvis ikke nogen grund til at have to referencer til dette formål, men det illustrerer at vorTabel og listen på lige fod refererer til det samme array i lagret.
	Man kan "genbruge" en reference ved at sætte den til at referere til et andet array.
Source 36: Gammel reference til nyt array	int[] vorTabel = new int[10]; int[] listen = vorTabel; vorTabel = new int[5]; System.out.println( vorTabel.length ); 5
	Her vil vorTabel i tredie linie blive sat til at referere til et nyt, og i dette tilfælde mindre, array efter først at have refereret til arrayet med de ti elementer, som listen nu er alene om at referere til.
	7. Fler-dimensionelle arrays
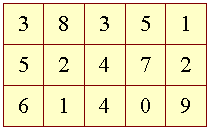
Illustrere med rækker og kolonner	Hidtil har vi kun set på en-dimensionelle arrays. Én-dimensionelle fordi de har ét index. Disse arrays har vi illustreret med en række af tal. Hvis vi i stedet ser på et to-dimensionelt array, har det to index, og kan illustreres med rækker og kolonner. F.eks.
Figur 6: Illustration af to-dimensionelt array
	Der kan erklæres med:
Source 37: Erklæring af to-dimensionelt array	int[][] toArray = new int[3][5];
	Som man ser, er det en ukompliceret udbygning af en-dimensionelle arrays. Med to index skal vi nu have to gange kantede paranteser i stedet for en gang kantede paranteser.
Begreberne rækker og kolonner er vores egen forståelse	Der er en ting man skal gøre sig klart fra starten: Java har ingen forståelse af hvad der er rækker og kolonner, det ligger alene i vores anvendelse. Det eneste vi her har angivet er at den første dimension er 3 og den anden dimension er 5.
	At vi, i dette tilfælde, ser på det som 3 rækker og 5 kolonner, er vores fortolkning, som vi derfor konsekvent må følge, hvis vi vil realisere denne sammenhæng. Dette ses bedst ved at vi initialiserer arrayet ved:
Source 38: initialisering af 3x5 array	int[][] toArray = { { 3, 8, 3, 5, 1 }, { 5, 2, 4, 7, 2 }, { 6, 1, 4, 0, 9 } };
	Dette skal læses på den måde at toArray er 3 i første dimension, derfor er de 3 talrækker adskilt med komma på yderste niveau. Dernæst er der 5 i anden dimension, derfor de 5 tal adskilt med komma, på næste niveau.
	Ovenstående erklærer ved initialisering et array med dimensionerne 3x5. Vi kunne lige så vel have oprettet de samme tal i et array med dimensionerne 5x3:
Source 39: initialisering af 5x3 array	int[][] toArray = { { 3, 5, 6 }, { 8, 2, 1 }, { 3, 4, 4 }, { 5, 7, 0 }, { 1, 2, 9 } };
	Det er kun et spørgsmål om hvordan vi selv ønsker sammenhængen med vores visuelle billede af et skema med række og kolonner. I det sidste tilfælde har vi valgt at kolonnerne skal være første dimension, mens rækkerne skal være anden dimension.
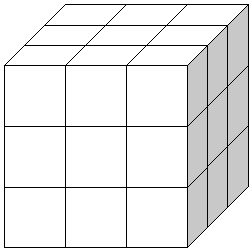
Flere dimensioner kræver flere kantede paranteser	Hvis vi vil have mere end to dimensioner, er det blot et spørgsmål om at tilføje flere kantede paranteser. Ved f.eks. tre dimensioner vil der visuelt være tale om en kubus.
Figur 7: Kubus
	Denne 3x3x3 kubus kan erklæres med
Source 40: Erklæring af tre-dimensionelt array	int[][][] kubus = new int[3][3][3];
	hvis vi fortsat antager, at der er tale om integers.
	Igen er det op til os selv, i vores anvendelse, at realisere hvad vi forstår ved de forskellige dimensioner.
Komma-niveauer	En initialisering af en sådan kubus forløber analogt til tidligere. På yderste komma-niveau har vi første dimension, på det næste den anden dimension osv. F.eks.:
Source 41: Erklæring med initialisering af tre-dimensionelt array	int[][][] kubus = { { { 1, 4, 3 }, { 9, 3, 6 }, { 0, 4, 6 } }, { { 7, 4, 8 }, { 7, 2, 5 }, { 8, 0, 1 } }, { { 2, 5, 7 }, { 5, 6, 2 }, { 1, 9, 0 } } };
	Blot er det nu vanskeligere at visualisere ud fra en sådan opstilling.
	7.1 Iteration over fler-dimensionelle arrays
	Lad os se et eksempel:
Source 42: Gennemløb af to-dimensionelt array	Eksempel: Udskriv et to-dimensionelt array int[][] toArray = { { 3, 8, 3, 5, 1 }, { 5, 2, 4, 7, 2 }, { 6, 1, 4, 0, 9 } }; for ( int række=0; række<3; række++ ) { for ( int kolonne=0; kolonne<5; kolonne++ ) System.out.print( toArray[række][kolonne] + " " ); System.out.println(); } 3 8 3 5 1 5 2 4 7 2 6 1 4 0 9
	Vi understreger vores forståelse af rækker og kolonner i denne anvendelse med passende variabel-navne. Det gør kildeteksten lettere at læse, men for compileren havde det naturligvis været det samme om de havde heddet i og j.
Lige så mange løkker inden i hinanden som der er dimensioner	Ligesom én løkke er typisk for gennemløb af et en-dimensionelt array, kendetegner to løkker inden i hinanden gennemløb af to-dimensionelle arrays. For hver indgang i den første dimension gennemløber den indre løkke den anden dimension.
	Hvis vi skal gennemløbe kubus'en kræver det derfor tre løkker inden i hinanden, da den er tre-dimensionel:
Source 43: Gennemløb af tre-dimensionelt array	Eksempel: Udskriv et tre-dimensionelt array for ( int højde=0; højde<3; højde++ ) for ( int bredde=0; bredde<3; bredde++ ) for ( int dybde=0; dybde<3; dybde++ ) System.out.print( kubus[højde][bredde][dybde] + " " );
	1 4 3 9 3 6 0 4 6 7 4 8 7 2 5 8 0 1 2 5 7 5 6 2 1 9 0
	7.2 Asymmetriske arrays
	Som noget specielt har java asymmetriske arrays.
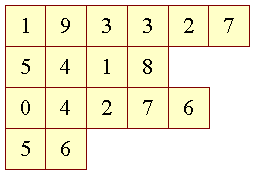
	Det asymmetriske ligger i, at ikke alle indgange i et fler-dimensionelt array behøver være lige lange. F.eks.
Figur 8: Assymetrisk array
	Dette asymmetriske to-dimensionelle array kan erklæres med følgende initialisering:
Source 44: Erklæring og initialisering af asymmetrisk array	int[][] asymArray = { { 1, 9, 3, 3, 2, 7 }, { 5, 4, 1, 8 }, { 0, 4, 2, 7, 6 }, { 5, 6 } };
	Ikke alene kan et sådant array kan være vanskeligere at anvende, det kræver også en forklaring. Hvordan kan det lade sig gøre?
Fler-dimensionelle arrays er arrays af arrays	Det skyldes at et to-dimensionelt array i virkeligheden er et array (første dimension) af arrays (anden dimension). Dvs. at vi ovenfor i virkeligheden har et en-dimensionelt array med fire elementer. Disse fire elementer er ikke integers, de er arrays. Det første element er et array med seks elementer, det andet element er et array med fire elementer osv. Hvis man ser på initialiseringen er det tydeligt, i særdeleshed fordi vi har valgt at placere hver række på en linie. Hvis man ser på typeangivelsen er det lidt mere skjult, men hvis man indfører paranteser (kun for illustrationens skyld, man må ikke gøre det i kildeteksten) bliver int[][] til (int[])[], altså et array (yderst) af arrays (inderste). Dette vil dog betyde en ombytning af index-rækkefølgen, så man skal kun se det som en illustration af, at der er tale om arrays af arrays, ikke som noget man konkret skal bruge til noget.
	7.2.1 Længder i asymmetriske arrays
	En anden vinkel som illustrerer der er tale om arrays af arrays er betydningen af length.
Source 45: length og fler-dimensionelt array	System.out.println( asymArray.length ); System.out.println( asymArray[0].length ); System.out.println( asymArray[1].length ); System.out.println( asymArray[2].length ); System.out.println( asymArray[3].length ); 4 6 4 5 2
	asymArray.length er 4 fordi der er 4 indgange i første dimension. Hver af disse indgange indeholder et array.
	asymArray[0] er det første af disse arrays og med asymArray[0].length får vi længden af den, nemlig 6. De efterfølgende tal illustrerer det asymmetriske ved de forskellige længder i anden dimension.
	7.2.2 Allokering af asymmetriske arrays
	Hvordan allokerer man et asymmetrisk array med new?
	Man gør det ved først at allokere den første dimension og efterfølgende at allokere arrays i næste dimension osv. Vi kan allokere asymArray ved følgende:
Source 46: Allokering af asymmetrisk array	int[][] asymArray; asymArray = new int[4][]; asymArray[0] = new int[6]; asymArray[1] = new int[4]; asymArray[2] = new int[5]; asymArray[3] = new int[2];
fodnoter:
1	I eksemplet anvender vi naturligvis iteration til beregning af denne sum, men summen kan også beregnes ud fra en grafisk observation og et integrale.
	Summen af tallene fra 1 til N kan beskrives som arealet af følgende histogram. Dvs. arealet af området mellem første-aksen og den trappeformede funktion (det farvelagte område).
Figur 9: Trappefunktion
	I figuren er også indtegnet identitetsfunktionen. Ved at tage integralet af den, kan vi finde størstedelen af arealet. Vi skal kun supplere med ½ for hver søjle, nemlig arealet af de små trekanter, som ligger over linien.
	Arealet, og dermed summen af tallene fra 1 til N, kan beregnes som:
	Repetitionsspørgsmål
1	Hvad betyder iteration?
2	Hvad er et array?
3	Hvad er index?
4	Hvad er en initialiseringsliste?
5	Hvordan refererer man til et element?
6	Hvordan allokeres et array?
7	Hvad vil det sige at et array er statisk?
8	Hvorfor bør man aldrig anføre et arrays længde som et literale?
9	Hvilken sætning ligner meget while-sætningen, rent syntaktisk?
10	Hvad er kørselsbetingelsen?
11	Hvad er et neutral-element?
12	Hvad er forskellen på while og do-while?
13	Hvornår kommer en anvendelse af do-while-sætningen til sin ret?
14	Er do-while-sætningen nødvendig?
15	Hvilke tre elementer har relation til tællervariabelen i forbindelse med tællerstyret iteration?
16	Hvad er fordelen ved for-sætningen frem for den tilsvarende while-sætning?
17	Hvad er standard-for-løkken?
18	Hvornår anvendes standard-for-løkken?
19	Hvad er sentinel-styret iteration, og hvad er sentinellen og sentinel-værdien?
20	Hvad er prisen for at anvende break og continue?
21	Hvad virker break og continue på?
22	Hvad gør break?
23	Hvilket problem kan der være med en tællervariabel i forbindelse med en for-løkke?
24	Hvad gør continue?
25	Hvad er sammenhængen mellem en reference-variabel og et array?
26	Hvordan allokerer man et to-dimensionelt array?
27	Hvordan forstår Java rækker og kolonner?
28	Hvordan opbygges initialiseringslisten for et fler-dimensionelt array?
29	Hvordan laver man et gennemløb af et fler-dimensionelt array?
30	Hvad er et asymmetrisk array?
31	Hvad er et fler-dimensionelt array i virkeligheden?
32	Hvordan finder man størrelsen af de forskellige dimensioner i et fler-dimensionelt array?
33	Hvordan allokerer man et asymmetrisk array?
	Svar på repetitionsspørgsmål
1	Gentagelse.
2	En tabel med data af samme type.
3	Hvert element i et array har et entydigt og fortløbende nummer, dette nummer kaldes index.
4	Et literale, der angiver hvilke data der intielt skal være i arrayet.
5	Man refererer til et element vha. dets index.
6	Det allokeres vha. new <type>[<størrelse>]; hvor type er elementernes type og størrelse er arrayets størrelse.
7	At det ikke kan ændre størrelse efter det er allokeret.
8	Fordi det gør koden statisk.
9	Syntaktisk ligner den if-sætningen - kun selve navnet er anderledes.
10	Den betingelse der skal være opfyldt så længe der itereres.
11	En operators neutral-element er det, for hvilket operatoren er uden "effekt", når det optræder som den ene operand.
12	do-while udfører altid sætningen mindst én gang. Efterfølgende er der ingen forskel.
13	F.eks. når kørselsbetingelsen ikke giver mening før den første interation.
14	Nej, den er kun syntaktisk sukker for en bestemt anvendelse af while-sætningen.
15	Initialisering, kørselsbetingelse og ændring.
16	At man på én linie kan overskue, hvad der styrer løkken.
17	En forløkke, hvis tæller, løber fra 0 til en vis værdi, med en ændring på +1 for hver iteration.
18	F.eks. Når man ønsker at køre et bestemt antal iterationer eller når man ønsker at gennemløbe et array.
19	Det er når en variabels værdi er afgørende for om der itereres. Variablen kaldes sentinellen og den værdi som den skal antage for at løkken terminerer kaldes sentinel-værdien.
20	Læsbarheden bliver forringet.
21	Alle iterative kontrol-strukturer og switch-sætningen.
22	Udførelsen af break bevirker at programudførelsen øjeblikkelig forlader kontrol-strukturen og forsætter efter denne.
23	Hvis den erklæres i for-løkkens hoved, vil dens virkefelt kun være selve for-løkken, og den vil derfor ikke eksistere efter for-løkken.
24	Den afbryder iterationen, og springer frem til en vurdering af om løkken skal køre igen (evaluering af kørselsbetingelsen).
25	En reference-variabel refererer til et array. F.eks. kan man godt have flere reference-variable, der refererer til det samme array.
26	Ved en simpel udbygning af syntaksen for allokering af et en-dimensionalt array. Man føjer ganske enkelt et sæt kantede parantereser til for hver dimension man ønsker mere.
27	Java forstår det overhovedet ikke! Det er op til os selv, i vores anvendelse, at realisere sådanne begreber. For java er der kun tale om dimensioner, som den ikke tillægger nogen rumlig betydning.
28	Ved en udbygning af syntaksen for initialieringslisten for et en-dimensionalt array; hvor man placerer initialiseringslister inden i hinanden i overensstemmelse med dimensionerne.
29	Ved at sætte flere for-løkker indeni hinanden.
30	Et array hvor ikke alle indgange har samme længde i samme dimension ("indgange" set ud fra den betragtning at fler-dimensionelle arrays er arrays af arrays).
31	Et array af arrays.
32	Vha. length, men man angiver kun index for de dimensioner der fører ud til den dimension man vil kende størrelsen af.
33	Man allokerer de enkelte del-arrays én efter én i de dimensioner der er asymmetriske.