© 1999-2003, Flemming Koch Jensen Alle rettigheder forbeholdt
Iteration Vejledning løsninger	Opgaver

 

 

	Iteration uden arrays (1-13)
1	Lav et program der beregner summen af tallene i intervallet [-10:10]. Opgaven kan løses med enten en while- eller en for-løkke, og ved enten at tælle op eller ned. Løs opgaven på alle fire måder.
~2	Lav et program der udskriver alle de ulige tal i intervallet [10:21].
~3	Lav et program der udskriver otte-tabellen.
4	n-fakultet (man skriver det n!) er defineret som produktet: 1*2*...*n. Lav et program der beregner n! af en variabel. Test: Du kan f.eks. bruge 5! = 120 til test af dit program
5	Lav et program der: Gennemløber alle tallene i intervallet [0:10] og udskriver om de er lige eller ulige, på formen: 0 er lige 1 er ulige 2 er lige 3 er ulige ... 10 er lige
6	Lav et program der udskriver summen af de ulige tal i intervallet [1:20].
7	Lav et program der: Erklærer to variable minimum og maximum, og sæt dem til henholdsvis 3 og 16. Udskriver antallet af lige og ulige tal i intervallet [minimum : maximum]. F.eks.: Der er 7 ulige og 7 lige tal i intervallet [3:16] Du skal lave en reel optælling i programmet. Test dit program med andre intervaller.
8	Lav et program der: Erklærer to variable minimum og maximum. Sætter minimum og maximum til værdier du selv vælger, således at minimum < maximum. Udskriver gennemsnittet af de lige tal i intervallet [minimum : maximum]. Løsningen skal laves med iteration og en reel beregning af gennemsnit med summering. F.eks.: for [9:15] er gennemsnittet 12, da (10+12+14)/3 = 12.
*9	Fibonacci-tallene er en særlig tal-følge: Nr. 1 2 3 4 5 6 7 8 9 10 Fibonacci-tal 1 1 2 3 5 8 13 21 34 55 Man ser her, at det første fibonacci-tal er 1, det andet er også 1, mens det tredie er 2. Idéen er, at man altid finder et bestemt fibonacci-tal ved at lægge de to foregående fibonacci-tal sammen. F.eks. er det 8'ende fibonacci-tal 21, fordi det 6'te og 7'ende er 8 og 13 ( 8 + 13 = 21 ) Lav et program der beregner det x'te fibonacci-tal, hvor x er en variabel i dit program hint: Brug flere variable
*10	Man kan regne fibonacci-tallene baglæns som det er gjort i følgende tabel: Nr. 2 1 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 Fibonacci-tal 1 1 0 1 -1 2 -3 5 -8 13 -21 34 -55 Man bruger det første og det andet fibonacci-tal (1 og 1) som basis for en beregning af det foregående fibonacci-tal 0. Lav et program der kan beregne det negative fibonacci-tal for en given negativ position. Dit program skal virke for værdier fra position 0 og nedefter hint: Du kan evt. løse opgaven på en lidt anden måde end der er lagt op til i beskrivelsen ovenfor. Sammenlign tabellen med tabellen fra den foregående opgave med fibonacci-tal, og observer en sammenhæng. Du kan udnytte denne observation til at iterere dig frem til løsningen, idet du bruger modulus og din løsning fra den foregående fibonacci-opgave, med lidt modifikationer. Løs opgaven, hvor du udnytter observationen i hintet, henholdsvis ikke gør det!
*11	Lav et program der: Erklærer en variable kandidat, og initialiserer den til en værdi fra intervallet [2:100] som du selv vælger. Udskriver om kandidat er et primtal. Et primtal er et tal, hvor om det gælder, at kun 1 og tallet selv går op i det. hint: brug modulus til at checke om der er andre tal end 1 og tallet selv der går op i kandidat.
~12	Lav et program der udskriver to-potenserne fra 2 til 1024. Dvs. dit program skal udskrive: 2 4 8 16 32 64 128 256 512 1024 De hedder to-potenser fordi de fremkommer som: 21, 22, 2 3, ... , 29, 2 10. hint: Opgaven kan løses meget enkelt. Tænk dig derfor godt om først!
13	Lav et program der udskriver den lille tabel (tallene fra 1 til 10 ganget med hinanden) på formen: 1 * 1 = 1 1 * 2 = 2 1 * 3 = 3 ... 1 * 10 = 10 2 * 1 = 2 2 * 2 = 4 ... 10 * 10 = 100 hint: Løs opgaven ved hjælp af to for-løkker, den ene inden i den anden.
	Iteration med en-dimensionelle arrays (14-39)
	I opgave 14-37, skal der anvendes en eller flere af følgende arrays, som copy/pastes ind i løsningen: int Ulige[] = { 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29 }; int Lige[] = { 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28 }; int Tabel[] = { 5, 8, 1, 9, 3, 6, 2, 3, 9, 4, 7, 5, 7, 2, 0, 1, 0, 2 }; int PosNeg[]= { 4, 9, -2, -6, 2, 6, -9, 4, 9, -1, 1, 0, -3, -3, 2, 7 }; int T1[] = { 44, 71, 93, 24, 35, 21, 64 }; int T2[] = { 32, 78, 12, 29, 21, 66, 92 }; int T3[] = { 25, 54, 62, 10, 99, 45, 23 }; int T4[] = { 36, 20, 71, 45, 94, 36, 41 }; int T5[] = { 53, 34, 31, 88, 85, 90, 11 };
~14	Lav et program der udskriver det første element fra Ulige[]
~15	Lav et program der udskriver længden af PosNeg[]
16	Lav et program der udskriver de fem første elementer af Tabel[]
17	Lav et program der udskriver alle elementerne fra T1[]
18	Lav et program der udskriver det midterste og det sidste element i T2[] Du må ikke direkte bruge det index som det pågældende element har, men skal bruge længden af arrayet og regne dig frem til index'et.
19	Lav et program der udskriver summen af elementerne fra PosNeg[]
20	Lav et program der udskriver alle de negative tal fra PosNeg[]
21	Lav et program der udskriver alle elementerne fra T3[] i omvendt rækkefølge, uden at ændre på array'et.
*22	Lav et program der ændrer i T4[], således at T4[]'s første tre elementer bliver de samme som de tre sidste i T5[]. De tre elementer skal stå i samme rækkefølge i T4[], som de gør i T5[]. Skal laves iterativt og ikke med tre assignments.
23	Lav et program der ændrer fortegn på alle elementerne i PosNeg[]. Udskriv de fire første og de fire sidste værdier som kontrol.
24	Lav et program der udskriver tallene fra 0 til 9. Du må kun udskrive værdier fra Lige[] og Ulige[], og tallene skal udskrives i stigende orden.
*25	Lav et program der vender rækkefølgen af elementerne i T3[], og bagefter udskriver elementerne, som kontrol. (Udskriften skal være den samme som i opgave 21)
26	Lav et program der tæller antal forekomster af tallet 7 i Tabel[]
27	Lav et program der beregner summen af alle de ulige positive tal i PosNeg[]
28	Lav et program der finder den største værdi i T1[]
*29	Lav et program der laver en statistik over hvor mange forekomster der findes i Tabel[] af de forskellige tal i intervallet [0:9], og udskriver denne statistikken på formen: Værdi Antal 0 2 1 2 ... 9 2   hint: Lav et array med ti elementer og brug det til at tælle i.
30	I PosNeg[] befinder der sig nogle negative tal. Lav et program der finder og udskriver det første af disse. Lav programmet i tre flere forskellige versioner, idet du anvender én af følgende: do/while-sætning for-sætning while-sætning
31	Lav et program der finder de to mindste værdier i T5[]
	I opgave 32-37, betegnes to elementer der står ved siden af hinanden som element-par. Man observerer at alle elementer danner par med deres to naboer, undtagen det første og sidste element der kun har én nabo og derfor kun indgår i ét par.
32	Lav et program der gennemløber T1[], og udskriver alle element-par. Udskriften skal være på formen: (44,71)(71,93)(93,24)(24,35)(35,21)(21,64)
33	Lav ændringer i dit program fra opgave 32, således at det gør følgende for hvert element-par: Hvis de to elementer er lige store gøres intet! Hvis de er forskellige tælles den mindste op med 1, og den største tælles ned med 1
34	Lav ændringer i dit program fra opgave 33, således at gennemløbet kan gentages flere gange. Det skal betyde at du f.eks. kan bestemme at array'et skal gennemløbes 3 gange; hvor der ved hvert gennemløb gøres som i opgave 33 Hvad sker der ved mange gennemløb af array'et?
35	Lav ændringer i dit program fra opgave 34, således at det i stedet gør følgende for hvert element-par Hvis de to elementer er lige store gøres stadig intet! Hvis de er forskellige sættes de begge til deres gennemsnit Du må gerne udnytte at gennemsnittet af to ens tal er tallet selv! Hvad sker der ved mange gennemløb i forhold til i opgave 34?
36	Lav ændringer i dit program fra opgave 35, således at det i stedet gør følgende ved hvert element-par Hvis de to elementer er lige store gøres stadig intet! Hvis elementet til venstre er mindre end elementet til højre gøres heller intet! Hvis elementet til venstre er større end elementet til højre byttes de to elementer om! Hvad sker der ved mange gennemløb?
37	Lav ændringer i dit program fra opgave 36, således at det automatisk stopper når array'et er sorteret Lav ændringer i dit program så det tæller hvor mange gange det har sammenlignet to elementer Effektiviser dit program så antallet af sammenligninger bliver mindst muligt
*38	Eratosthenes (græker, 273-194 fvt., den første der beregnede Jordens omkreds, fra år 240 leder af det berømte Alexandrinske bibliotek) fandt på en meget hurtig, men pladskrævende måde, at finde alle primtal op til en vis øvre grænse, f.eks. alle primtal i intervallet [0:100] Idéen er at starte med et array hvor alle elementer er sat til en bestemt værdi, f.eks. 0 (elementerne med index 0 og 1 sættes dog til 1). Dernæst betyder 0 at vi endnu ikke har konstateret at det pågældende index ikke skulle være et primtal, og tallet 1 at vi endegyldigt har konstateret at det pågældende index ikke er et primtal (Fra start har vi netop konstateret at 0 og 1 ikke er primtal, mens det stadig er et åbent spørgsmål for resten!) Dernæst starter man en iterativ proces hvor man hele tiden finder det næste index, der har element 0, sætter alle multiplum af det pågældende index til 1 og dernæst går videre med det næste index der stadig har et element med værdien 0 Hvis vi anvender et lille array med 12 indgange, vil forløbet for de første iterationer se ud som følger: Det initielle array: 0 1 2 3 4 5 6 7 8 9 10 11 1 1 0 0 0 0 0 0 0 0 0 0 Vi konstaterer at 2 er det første index med et element 0, og vi sætter alle multiplum af 2 til 1: 0 1 2 3 4 5 6 7 8 9 10 11 1 1 0 0 1 0 1 0 1 0 1 0 Vi konstaterer at 3 er det næste index med et element 0, og vi sætter alle multiplum af 3 til 1: 0 1 2 3 4 5 6 7 8 9 10 11 1 1 0 0 1 0 1 0 1 1 1 0   Vi konstaterer at 5 er det næste index med et element 0, og vi sætter alle multiplum af 5 til 1: 0 1 2 3 4 5 6 7 8 9 10 11 1 1 0 0 1 0 1 0 1 1 1 0 Og således fortsætter man. Lav et program der finder primtallene i intervallet [0:100] og udskriver dem. hint: I forbindelse med test kan du evt. anvende, at der er 25 primtal i intervallet [0:100]. Når du har løst opgaven, så lav ændringer i dit program så du arbejder med et array af booleans. Ekperimenter endvidere med hvor store arrays, der kan bearbejdes inden for rimelig tid.
*39	I denne opgave skal vi lave verdens simpleste og hurtigste form for sortering: Bucket sort. På trods af de fine titler er det faktisk også en af de simpleste sorterings-algoritmer at implementere.
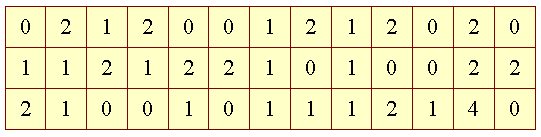
	Hvis vi f.eks. skulle sortere elementerne i følgende array:
	3 3 9 5 2 6 0 2 1 7 4 8 2 4
	Så kunne vi lave en statistik i et andet array, over hvor mange forekomster, der er af hvert tal i intervallet [0:9]:
	0 1 2 3 4 5 6 7 8 9 1 1 3 2 2 1 1 1 1 1
	Det kan man "hælde" tilbage i det oprindelige array, ved at starte med én 0'er, én 1'er, tre 2'ere, to 3'ere osv. Derved ville de oprindelige værdier blive overskrevet og arrayet vil i stedet blive:
	0 1 2 2 2 3 3 4 4 5 6 7 8 9
	Lav en implementation af bucket sort, der sorterer følgede array:
	int[] t = { 3, 8, 9, 4, 3, 6, 5, 4, 1, 7, 2, 8, 7, 6, 9, 4, 5, 2, 6, 1, 0, 4, 9, 7, 8, 6, 2, 4, 9, 2 };
	Iteration med fler-dimensionelle arrays (40-)
40	Lav et program der indsætter den lille tabel i et to-dimensionelt array og dernæst udskriver den fra tabellen.
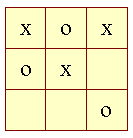
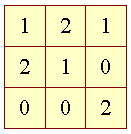
41	I et spil kryds og bolle kan situationen være følgende: Brættet kan repræsenteres som et to-dimensionelt array med følgende udssende: Hvor 0 er et tomt felt, 1 er et kryds og 2 er en bolle: Lav et program der erklærer det to-dimensionelle array ovenfor og udskriver det på formen: XOX OX O
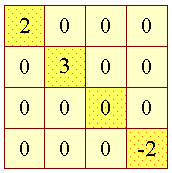
42	Betragt følgende kvadratiske to-dimensionelle array: De markerede felter kaldes diagonalen. Hvis alle felter der ikke ligger på diagonalen er 0, kalder man det en diagonal-matrice. Man observer at ovenstående er en diagonal-matrice. Lav et program der undersøger om et vilkårligt kvadratisk to-dimensionelt array af integers er en diagonal-matrice.
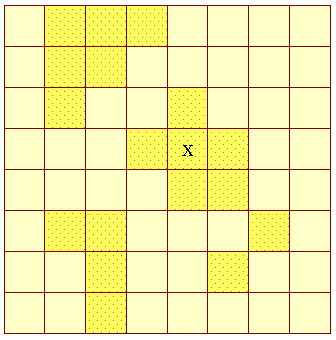
43	Betragt følgende figur: Nogle af felterne er markerede. Ud over det har vi sat et kryds i et af de markerede felter (udelukkende for at vi kan referere til det her). Feltet er nemlig specielt - det er et såkaldt krydsfelt. Et krydsfelt er et felt der er markeret og som har markerede felter til alle sider (dvs. de fire felter til højre/venstre og ovenover/nedenunder). Man bemærker at ingen felter på "randen" kan være krydsfelter, da de alle mangler en eller flere nabofelter. Man kan repræsentere felterne som elementer i et to-dimensionelt array af booleans, hvor true betyder at et felt er markeret. Lav et program der erklærer ovenstående array og udskriver index for samtlige krydsfelter.
*44	I et tipsprogram har man behov for at kunne udskrive en tipskupon. En tipskupon er givet ved et to-dimensionelt array, hvor første dimension er tipsrækken og anden dimension er kampen. Lav et program der udskriver en tipdskupon. F.eks. følgende array med 3 tipsrækker og 13 kampe: Hvor 1 og 2 svarer til tegnene "1" og "2", og 0 svarer til "X". Programmet skal lave en udskrift med følgende udseende: 1| X |1 | 2| 2| 2|1 |1 | 3|1 | 2| X | 4| 2|1 | X | 5| X | 2|1 | 6| X | 2| X | 7|1 |1 |1 | 8| 2| X |1 | 9|1 |1 |1 | 10| 2| X | 2| 11| X | X |1 | 12| 2| 2|???| 13| X | 2| X | Bemærk, at der udskrives ???, som indikation af, at tallet ikke kan fortolkes som et tipstegn. Du skal erklære et array svarende til det i eksemplet ovenfor, med en initialiseringsliste så dimensionerne passer med den fortolkning, der er beskrevet. Dernæst skal programmet foretage udskriften.